题目内容
直角梯形ABCD中,AD∥BC,∠B=90°,AD+BC<DC,若腰DC上有一点P,使AP⊥BP,则这样的点
- A.不存在
- B.只有一个
- C.只有两个
- D.有无数个
C
分析:由题意可得使AP⊥BP的点P在以AB为直径的圆上,根据圆与BC的位置关系即可得解.
解答: 解:这样的点有2个.
解:这样的点有2个.
∵AP⊥BP,
∴P在以AB为直径的圆上,令圆心为O.
当CD切⊙O于点P时,
则OP⊥CD,
∵AD∥BC、∠B=90°,
∴∠A=90°,
∴AD切⊙O于点A、BC切⊙O于点B,
∴由切线长定理得:AD=DP、BC=CP,
∴此时AD+BC=DP+CP=DC.
∵AD+BC<DC,可理解为将DC由与⊙O相切时的位置向靠近圆心方的向平移,这样,⊙O与DC就相交了.
∴有两个交点.
故选C.
点评:本题考查了直角梯形的性质、圆与直线的位置关系,是一道考查学生综合知识运用能力的中档题.
分析:由题意可得使AP⊥BP的点P在以AB为直径的圆上,根据圆与BC的位置关系即可得解.
解答:
 解:这样的点有2个.
解:这样的点有2个.∵AP⊥BP,
∴P在以AB为直径的圆上,令圆心为O.
当CD切⊙O于点P时,
则OP⊥CD,
∵AD∥BC、∠B=90°,
∴∠A=90°,
∴AD切⊙O于点A、BC切⊙O于点B,
∴由切线长定理得:AD=DP、BC=CP,
∴此时AD+BC=DP+CP=DC.
∵AD+BC<DC,可理解为将DC由与⊙O相切时的位置向靠近圆心方的向平移,这样,⊙O与DC就相交了.
∴有两个交点.
故选C.
点评:本题考查了直角梯形的性质、圆与直线的位置关系,是一道考查学生综合知识运用能力的中档题.

练习册系列答案
相关题目
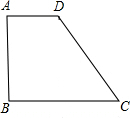 在直角梯形ABCD中,底AD=6cm,BC=11cm,腰CD=12cm,则这个直角梯形的周长为
在直角梯形ABCD中,底AD=6cm,BC=11cm,腰CD=12cm,则这个直角梯形的周长为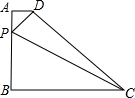 如图,直角梯形ABCD中,AD∥BC,∠B=90°,AD=1,BC=8,AB=6,点P在高AB上滑动,当AP长为
如图,直角梯形ABCD中,AD∥BC,∠B=90°,AD=1,BC=8,AB=6,点P在高AB上滑动,当AP长为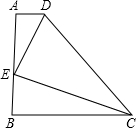 下结论:
下结论: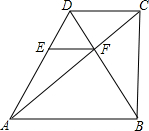 EF∥AB,交AD于点E,CF=4cm.
EF∥AB,交AD于点E,CF=4cm.