题目内容
 如图,已知D是线段BC上的一点,如果添加条件∠DAC=∠ABC,可得到结论:
如图,已知D是线段BC上的一点,如果添加条件∠DAC=∠ABC,可得到结论: =________.在划线中填写一个结论并证明.
=________.在划线中填写一个结论并证明.

分析:因为三角形ADC与三角形ABC的边DC与BC边上的高是同一条,所以根据三角形的面积公式得到三角形ADC与三角形ABC的面积之比为DC:BC,即为所求的比值,又根据已知的两角相等,且∠ACB为公共角,由两对对应角相等的两三角形相似,得到三角形ADC与三角形ABC相似,得到对应边之比等于相似比,面积之比等于相似比的平方,故得到所求式子的比值等于三角形ADC与三角形ABC相似比的平方,所以找出两相似三角形的一对对应边即可.
解答:
 (只需写一个即可)
(只需写一个即可)
证明:过A作AE⊥BC,交BC于点E,
∵S△ADC=
 DC•AE,S△ABC=
DC•AE,S△ABC= BC•AE,
BC•AE,∴
 ,
,又∵∠DAC=∠ABC,∠ACB=∠DCA,
∴△ADC∽△BAC,
∴
 ,
,∵
 ,
,∴
 .
.故答案为:
 .
.点评:此题考查了相似三角形的判定与性质,要求学生掌握相似三角形的对应边之比等于相似比,对应面积之比等于相似比的平方,把所求式子的比根据高为同一条高,转化为两三角形的面积之比是解本题的关键.此题属于开放型题,答案不确定,只需满足题意的任意一个即可.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
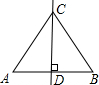 如图,已知CD是线段AB的垂直平分线,垂足为D,E是CD上一点.若∠A=60°,则下列结论中错误的是( )
如图,已知CD是线段AB的垂直平分线,垂足为D,E是CD上一点.若∠A=60°,则下列结论中错误的是( )| A、AE=BE | B、AD=BD | C、AB=AC | D、ED=AD |
如图,已知C是线段AB的中点,则CD等于( )


| A、AD-BD | ||
B、
| ||
C、
| ||
D、AD-
|
 如图,已知B是线段AE上一点,ABCD和BEFG都是正方形,连接AG、CE.
如图,已知B是线段AE上一点,ABCD和BEFG都是正方形,连接AG、CE. (2012•宿迁)如图,已知P是线段AB的黄金分割点,且PA>PB,若S1表示PA为一边的正方形的面积,S2表示长是AB,宽是PB的矩形的面积,则S1
(2012•宿迁)如图,已知P是线段AB的黄金分割点,且PA>PB,若S1表示PA为一边的正方形的面积,S2表示长是AB,宽是PB的矩形的面积,则S1