Question

在研究“三角形的三个内角和等于180°”的证明方法时，小明和小虎分别给出了下列证法：

小明：在△ABC中，延长BC到点D(如图)，

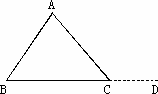
所以∠ACD＝∠A＋∠B．(三角形的一个外角等于与它不相邻的两个内角的和)

又因为∠ACD＋∠ACB＝180°，(平角定义)

所以∠A＋∠B＋∠ACB＝180°．(等量代换)

小虎：在△ABC中，过点A作AD⊥BC(如图)，

所以∠ADC＝∠ADB＝90°．(直角定义)

所以∠DAC＋∠C＝90°，∠B＋∠BAD＝90°．(直角三角形的两锐角互余)

所以∠DAC＋∠C＋∠B＋∠BAD＝180°，

即∠BAC＋∠B＋∠C＝180°．

请你对上述两名同学的证法给出评价，并写出一种你认为较简单的证明三角形内角和定理的方法．

Answer 1

答案：
解析：

解：两名同学的证法都不对．因为“三角形的一个外角等于与它不相邻的两个内角的和”与“直角三角形的两锐角互余”都是由三角形内角和定理推导得到的． 　　证明方法不唯一，只要正确即可． 　　证明：如下图，过点A作EF∥BC， 　　所以∠EAB＝∠B，∠FAC＝∠C．(两直线平行，内错角相等) 　　因为∠EAB＋∠BAC＋∠FAC＝180°，(平角定义) 　　所以∠B＋∠BAC＋∠C＝180°．