题目内容
6. 如图,函数y=3x和y=ax+4的图象相交于点A(m,3),不等式3x≥ax+4的解集为x≥1.
如图,函数y=3x和y=ax+4的图象相交于点A(m,3),不等式3x≥ax+4的解集为x≥1.
分析 首先利用待定系数法求出A点坐标,再以交点为分界,结合图象写出不等式3x≥ax+4的解集即可.
解答 解:将点A(m,3)代入y=3x得,3m=3,
解得,m=1,
所以点A的坐标为(1,3),
由图可知,不等式3x≥ax+4的解集为x≥1.
故答案为x≥1.
点评 此题主要考查了一次函数与一元一次不等式的关系:从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.关键是求出A点坐标以及利用数形结合的思想.

练习册系列答案
相关题目
17.下列说法不正确的是( )
| A. | 球的截面一定是圆 | |
| B. | 组成长方体的各个面中不可能有正方形 | |
| C. | 从三个不同的方向看正方体,得到的都是正方形 | |
| D. | 圆锥的截面可能是圆 |
11.分式$\frac{x}{4a}$,$\frac{x-y}{{x}^{2}-{y}^{2}}$,$\frac{a+b}{a-b}$,$\frac{(x+y)^{2}}{xy+{y}^{2}}$,$\frac{4}{2x-6}$中,最简分式的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
18.下列方程组中,是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{2x-y=7}\\{3y=2x-3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=1}\\{xy=12}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{\frac{y}{3}-\frac{x}{2}-1}\\{2{x}^{2}+3y-15}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{1}{x}-\frac{2}{y}=1}\\{x+y=10}\end{array}\right.$ |
16.若(m-3)2+$\sqrt{n+2}$=0,则m+n的平方根是( )
| A. | 1 | B. | ±1 | C. | $\sqrt{5}$ | D. | ±$\sqrt{5}$ |
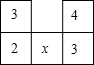 如图所示是由几个相同的小正方体所组成的几何体的俯视图,小正方形中的数字表示在该位置的小正方体的个数,请画出这个几何体从正面看和从左面看到的图形,其中x是平方等于本身的正整数.
如图所示是由几个相同的小正方体所组成的几何体的俯视图,小正方形中的数字表示在该位置的小正方体的个数,请画出这个几何体从正面看和从左面看到的图形,其中x是平方等于本身的正整数.