题目内容
对于等式y=ax2+bx+c,有三对x,y的值
;
;
能使等式两边值相等,试求a,b,c的值.
|
|
|
分析:把三对x,y的值分别代入y=ax2+bx+c得到得
,由②-①得a-b=2④,③-②得a+b=0⑤,再解由④⑤组成的方程组,求出a、b,然后把a、b的值代入①可求出c.
|
解答:解:根据题意得
,
②-①得3a-3b=6,整理得a-b=2④,
③-②得5a+5b=0,整理得a+b=0⑤,
解由④⑤组成的方程组
得
,
把a=1,b=-1代入①得1-1+c=-2,
解得c=-2,
所以原方程组的解为
.
|
②-①得3a-3b=6,整理得a-b=2④,
③-②得5a+5b=0,整理得a+b=0⑤,
解由④⑤组成的方程组
|
|
把a=1,b=-1代入①得1-1+c=-2,
解得c=-2,
所以原方程组的解为
|
点评:本题考查了解三元一次方程组:利用加减消元或代入消元法把三元一次方程转化为二元一次方程.

练习册系列答案
相关题目
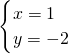 ;
; ;
; 能使等式两边值相等,试求a,b,c的值.
能使等式两边值相等,试求a,b,c的值.