题目内容
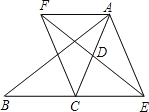
【题目】已知:如图所示的一张矩形纸片![]() , 将纸片折叠一次,使点A与C重合,再展开, 折痕EF交AD边于E,交BC边于F,分别连结AF和CE.
, 将纸片折叠一次,使点A与C重合,再展开, 折痕EF交AD边于E,交BC边于F,分别连结AF和CE.
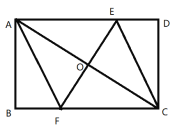
(1)求证:四边形AFCE是菱形;
(2)在线段AC上是否存在一点P,使得![]() ?若存在,请说明点P的位置,并予以证明;若不存在,请说明理由.
?若存在,请说明点P的位置,并予以证明;若不存在,请说明理由.
【答案】(1)见解析;(2)存在,过点E作AD的垂线,交AC于点![]() ,点
,点![]() 就是符合条件的点,见解析
就是符合条件的点,见解析
【解析】
(1)由折叠的性质得出EF垂直平分AC,OA=OC,由矩形的性质得出∠B=90°,AD∥BC,得出∠![]() ∠
∠![]() ,∠EAO=∠FCO,由ASA证明△AOE≌△COF,得出AE=CF,证出四边形AFCE是平行四边形,即可得出结论;
,∠EAO=∠FCO,由ASA证明△AOE≌△COF,得出AE=CF,证出四边形AFCE是平行四边形,即可得出结论;
(2)过E作EP⊥AD交AC于P,则P就是所求的点.则∠AEP=90°,证出△AOE∽△AEP,得出对应边成比例![]() ,则AE2=AOAP,再由AO=
,则AE2=AOAP,再由AO=![]() AC,即可得出结论.
AC,即可得出结论.
(1)证明:在矩形ABCD中, AD∥BC
∴ ∠![]() ∠
∠![]() ,∠
,∠![]() =∠
=∠![]()
由折叠可知:OA=OC![]()
∴ △![]() ≌△
≌△![]()
∴ AE=CF,
又AE∥CF
∴ 四边形![]() 是平行四边形
是平行四边形
又由折叠可知:AF=CF,![]()
∴ 四边形![]() 是菱形.
是菱形.
(2)存在,过点E作AD的垂线,交AC于点![]() ,点
,点![]() 就是符合条件的点.
就是符合条件的点.
理由如下:
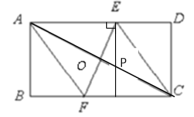
由作法得:∠AEP=90°,
由(1)得:AC⊥EF,
∴∠![]() 90°
90°
∴∠![]() ∠
∠![]() 90°,
90°,
又∵∠![]() ∠
∠![]()
∴ △![]() ∽△
∽△![]()
∴ ![]()
∴AE2=AOAP,
∵AO=![]() AC,
AC,
∴AE2=![]() ACAP
ACAP
即:![]() .
.

练习册系列答案
相关题目
【题目】抛物线![]() 上部分点的横坐标
上部分点的横坐标![]() ,纵坐标
,纵坐标![]() 的对应值如下表:
的对应值如下表:
| … |
|
|
|
|
| … |
| … |
|
|
|
|
| … |
![]() 根据上表填空:
根据上表填空:
①抛物线与![]() 轴的交点坐标是________和________;
轴的交点坐标是________和________;
②抛物线经过点![]() ,________
,________![]() ;
;
③在对称轴右侧,![]() 随
随![]() 增大而________;
增大而________;
![]() 试确定抛物线
试确定抛物线![]() 的解析式.
的解析式.