题目内容
已知a，b为实数，且满足b2+
+36=12b，
（1）若a，b为△ABC的两边，求第三边c的取值范围；
（2）若a，b为△ABC的两边，第三边c=10，求△ABC的面积．
| a-8 |
（1）若a，b为△ABC的两边，求第三边c的取值范围；
（2）若a，b为△ABC的两边，第三边c=10，求△ABC的面积．
考点：配方法的应用,非负数的性质：偶次方,非负数的性质：算术平方根,三角形三边关系,勾股定理的逆定理
专题：计算题
分析：已知等式整理后，利用完全平方公式变形，再利用非负数的性质求出a与b的值，
（1）利用三角形三边关系求出c的范围即可；
（2）利用勾股定理的逆定理得到三角形为直角三角形，求出面积即可．
（1）利用三角形三边关系求出c的范围即可；
（2）利用勾股定理的逆定理得到三角形为直角三角形，求出面积即可．
解答：解：已知等式变形得：b2-12b+36+
=（b-6）2+
=0，
∴b=6，a=8，
（1）第三边c的范围为2＜c＜14；
（2）∵62+82=102，
∴△ABC为直角三角形，
则△ABC面积为
×6×8=24．
| a-8 |
| a-8 |
∴b=6，a=8，
（1）第三边c的范围为2＜c＜14；
（2）∵62+82=102，
∴△ABC为直角三角形，
则△ABC面积为
| 1 |
| 2 |
点评：此题考查了配方法的应用，非负数的性质，三角形三边关系，以及勾股定理的逆定理，熟练掌握完全平方公式是解本题的关键．
练习册系列答案
相关题目
已知△ABC为等边三角形，BD为中线，延长BC至E，使CE=CD=1，连接DE，求：三角形三个内角的度数分别是（x+y）°，（x-y）°，x°，且x＞y＞0，则该三角形有一个内角为（ ）
| A、30° | B、45° |
| C、90° | D、60° |
有下列长度的三条线段，能组成等腰三角形的是（ ）
| A、2cm，2cm，4cm |
| B、3cm，8cm，3cm |
| C、3cm，4cm，6cm |
| D、5cm，4cm，4cm |
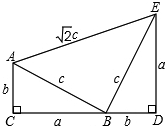四边形ACDE是证明勾股定理用到的一个图形，a，b，c是Rt△ABC和Rt△BED边长，易知AE=