题目内容
如图,反比例函数 (x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB=
(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB= ,将线段AB沿x轴正方向平移到线段DC的位置,反比例函数
,将线段AB沿x轴正方向平移到线段DC的位置,反比例函数 (x>0)的图象恰好经过DC的中点E。
(x>0)的图象恰好经过DC的中点E。
(1)求k的值和直线AE的函数表达式;
(2)若直线AE与x轴交于点M、与y轴交于点N,请你探索线段AN与线段ME的大小关系,写出你的结论并说明理由.

(1)由已知得,在Rt△OAB中,OB=2,tan∠AOB= ,∴
,∴ =
= ,∴AB=3,∴A点的坐标为(2,3)∴k=xy=6 ;∵DC由AB平移得到,点E为DC的中点,
,∴AB=3,∴A点的坐标为(2,3)∴k=xy=6 ;∵DC由AB平移得到,点E为DC的中点,
∴点E的纵坐标为 ,又∵点E在双曲线
,又∵点E在双曲线 上,∴点E的坐标为(4,
上,∴点E的坐标为(4, )设直线MN的函数表达式为y=k1x+b,则
)设直线MN的函数表达式为y=k1x+b,则 , 解得
, 解得 ,
,
∴直线MN的函数表达式为 。…
。…
(2)结论:AN=ME
理由:在表达式 中,令y=0可得x=6,令x=0可得y=
中,令y=0可得x=6,令x=0可得y= ,∴点M(6,0),N(0,
,∴点M(6,0),N(0, )…1分
)…1分
 解法一:延长DA交y轴于点F,则AF⊥ON,且AF=2,OF=3,
解法一:延长DA交y轴于点F,则AF⊥ON,且AF=2,OF=3,
∴NF=ON-OF =
= ,∵
,∵ CM=6-4=2=AF,EC=
CM=6-4=2=AF,EC= =NF,
=NF,
∴Rt△ANF≌Rt△MEC,∴AN=ME
解法二:延长DA交y轴于点F,则AF⊥ON,且AF=2,OF=3,
∴NF=ON-OF= ,∴根据勾股定理可得AN=
,∴根据勾股定理可得AN= ,∵CM=6-4=2,EC=
,∵CM=6-4=2,EC= ∴根据勾股定理可得EM=
∴根据勾股定理可得EM= ∴AN=ME…
∴AN=ME…
解法三:连接OE,延长DA交y轴于点F,则AF⊥ON,且AF=2,
∵S△EOM ,S△AON
,S△AON
∴S△EOM= S△AON,∵AN和ME边上的高相等,∴AN=ME…

 阅读快车系列答案
阅读快车系列答案目前我们生活垃圾一般可分为四大类:可回收垃圾、厨余垃圾、有害垃圾和其他垃圾。为了有效保护环境和节约资源,杭州在每一试点区将垃圾桶分可回收垃圾桶、厨余垃圾桶、有害垃圾桶和其他垃圾桶供市民们投放。并免费发放印有区分垃圾的垃圾袋供市民使用。一星期后对这些小区的垃圾进行了抽样调查。发现
| 垃圾桶 | 垃圾数 | 比例 |
| 可回收垃圾桶 | 420 | |
| 厨余垃圾桶 | 630 | 37.5% |
| 有害垃圾桶 | ||
| 其他垃圾桶 | 11.25% |

(1) 补全两个表中的空缺部分;
(2) 一天小明拿着四个分别装有可回收垃圾、厨余垃圾、有害垃圾和其他垃圾的垃圾袋去扔垃圾,问在小明随意将四袋垃圾分别扔进四个垃圾桶的情况下,四袋垃圾都扔错的概率是多少?
 )
)

 ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=
ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG= ,则ΔCEF的面积为( )
,则ΔCEF的面积为( )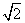 B.
B. C.
C. D.
D.


 B.3.59×
B.3.59× A. 2月 B. 5月 C. 6月 D. 7月
A. 2月 B. 5月 C. 6月 D. 7月 m B.
m B.  m C.
m C.  m D.
m D.  m
m