题目内容
 如图,G是边长为4的正方形ABCD边上一点,矩形DEFG的边EF经过点A,已知GD=5,则矩形DEFG的面积为________.
如图,G是边长为4的正方形ABCD边上一点,矩形DEFG的边EF经过点A,已知GD=5,则矩形DEFG的面积为________.
16
分析:连接AG,根据△ADG面积既是正方形ABCD的面积的一半,又是矩形EFGD的面积的一半,根据面积相等计算矩形的边长FG,利用矩形的面积公式即可求出矩形DEFG的面积.
解答:如图,连接AG,则SABCD=2S△ADG,
SDEFG=2S△ADG,
∴SABCD=SDEFG,即42=5•FG
∴FG= ,
,
∴矩形DEFG的面积=5× =16,
=16,
故答案为16.
点评:本题考查了正方形、矩形面积计算方法,巧妙地连接AG使得△ADG面积既是正方形ABCD的面积的一半,又是矩形EFGD的面积的一半是解题的关键.
分析:连接AG,根据△ADG面积既是正方形ABCD的面积的一半,又是矩形EFGD的面积的一半,根据面积相等计算矩形的边长FG,利用矩形的面积公式即可求出矩形DEFG的面积.
解答:如图,连接AG,则SABCD=2S△ADG,
SDEFG=2S△ADG,

∴SABCD=SDEFG,即42=5•FG
∴FG=
 ,
,∴矩形DEFG的面积=5×
 =16,
=16,故答案为16.
点评:本题考查了正方形、矩形面积计算方法,巧妙地连接AG使得△ADG面积既是正方形ABCD的面积的一半,又是矩形EFGD的面积的一半是解题的关键.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
 14、如图,O是边长为6的等边三角形ABC内的任意一点,且OD∥BC,交AB于点D,OF∥AB,交AC于F,OE∥AC,交BC于E.则OD+OE+OF的值( )
14、如图,O是边长为6的等边三角形ABC内的任意一点,且OD∥BC,交AB于点D,OF∥AB,交AC于F,OE∥AC,交BC于E.则OD+OE+OF的值( )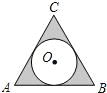 如图,⊙O是边长为2的等边三角形ABC的内切圆,则图中阴影部分的面积为
如图,⊙O是边长为2的等边三角形ABC的内切圆,则图中阴影部分的面积为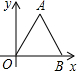 如图,△AOB是边长为5的等边三角形,则A,B两点的坐标分别是A
如图,△AOB是边长为5的等边三角形,则A,B两点的坐标分别是A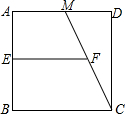 如图,M是边长为2cm的正方形ABCD的边AD的中点,E、F分别是AB、CM的中点.则EF=
如图,M是边长为2cm的正方形ABCD的边AD的中点,E、F分别是AB、CM的中点.则EF= 如图,△ABC是边长为6的等边三角形,AD=2,AE∥BC,直线BD交AE于点E,则BE的长为( )
如图,△ABC是边长为6的等边三角形,AD=2,AE∥BC,直线BD交AE于点E,则BE的长为( )