题目内容
十二五”期间是宁波市加快发展现代渔业的重要时期,为适应市场需求,某水产养殖场兴建了标准化高效健康养殖示范区,计划今年养殖梭子蟹和南美白对虾,由于受养殖水面的制约,这两种品种的苗种的总投放量只有50吨,根据经验测算,这两种品种的种苗每投放一顿的先期投资、养殖期间的投资以及产值如表所示:(单位:千元/吨)
| 品种 | 先期投资 | 养殖期间的投资 | 产值 |
| 梭子蟹 | 9 | 3 | 30 |
| 南美白对虾 | 4 | 10 | 20 |
(1)要使产值达到1350千克,问梭子蟹和南美白对虾各应养殖多少吨?
(2)若养殖场先期投资不超过360千元,养殖期间的投资不超过290千元,设梭子蟹种苗的投放量为x吨.
①求x的取值范围;
②设这两个品种产出后的总产值为y(千元),试写出y与x之间的函数解析式,当x等于多少时,y有最大值?最大值是多少?
解:(1)设梭子蟹种苗的投放量为x吨,则南美白对虾的投放量为(50﹣x)吨,
根据题意得:30x+20(50﹣x)=1350,
解得x=35,
50﹣35=15.
答:要使产值达到1350千克,梭子蟹应养殖35吨,南美白对虾应养殖15吨.
(2)①依题意得
∴x的取值范围是30≤x≤32;
②设这两个品种产出后的总产值为y千元
y=30x+20(50﹣x)=10x+1000,
∵k=10>0,
∴y随x的增大而增大,
又∵30≤x≤32,
故当x=32时,y最大=10×32+1000=1320
答:当x等于32时,这两个品种产出后的总产值为最大,最大值是1320千元.

练习册系列答案
相关题目
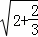 =2
=2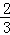 ,验证:
,验证: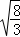 =
=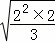 =2
=2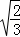 .
.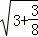 =3
=3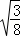 ,验证:
,验证: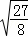 =
=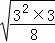 =3
=3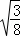 .
.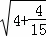 的变形结果并进行验证;
的变形结果并进行验证; ⊗1=1,则x的取值范围是
⊗1=1,则x的取值范围是 
 B.
B.  C. 1 D.
C. 1 D. 
 >
>
 有两个不相等的实数根时,试确定m的取值范围.
有两个不相等的实数根时,试确定m的取值范围.