题目内容
19.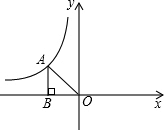 如图,A是反比例函数图象上第二象限内的一点,且△ABO的面积为3,则反比例函数的解析式是y=-$\frac{6}{x}$.
如图,A是反比例函数图象上第二象限内的一点,且△ABO的面积为3,则反比例函数的解析式是y=-$\frac{6}{x}$.
分析 根据反比例函数系数k的几何意义可知,△ABO的面积=$\frac{1}{2}$|k|,再根据图象所在象限 求出k的值既可.
解答 解:依据比例系数k的几何意义可得,△ABO的面积=$\frac{1}{2}$|k|,
即$\frac{1}{2}$|k|=3,
解得,k=±6,
由于函数图象位于第二象限,
故k=-6,
函数解析式为y=-$\frac{6}{x}$.
故答案为:y=-$\frac{6}{x}$.
点评 本题考查反比例函数系数k的几何意义,关键是熟记过双曲线上的任意一点分别向两条坐标轴作垂线,与坐标轴围成的矩形面积就等于|k|.

练习册系列答案
相关题目
9.经过一、二、三象限的某一次函数的图象上有A(1,m)、B(-1,n)两点,则( )
| A. | m<0 | B. | n<0 | C. | m+n>0 | D. | m+n>1 |
10.-$\frac{1}{2}$的倒数为( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | -2 |
7.27的立方根是( )
| A. | -3 | B. | -9 | C. | 3 | D. | 9 |
14.一个两位数的个位数字是a,十位数字是b,则这个两位数可表示为( )
| A. | ab | B. | a+b | C. | 10a+b | D. | 10b+a |
4. 如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C;直线DF分别交l1,l2,l3于点D、E、F,AC与DF相交于点H,且AH=2,HB=1,BC=5,则$\frac{DE}{EF}$=( )
如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C;直线DF分别交l1,l2,l3于点D、E、F,AC与DF相交于点H,且AH=2,HB=1,BC=5,则$\frac{DE}{EF}$=( )
 如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C;直线DF分别交l1,l2,l3于点D、E、F,AC与DF相交于点H,且AH=2,HB=1,BC=5,则$\frac{DE}{EF}$=( )
如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C;直线DF分别交l1,l2,l3于点D、E、F,AC与DF相交于点H,且AH=2,HB=1,BC=5,则$\frac{DE}{EF}$=( )| A. | $\frac{3}{5}$ | B. | 2 | C. | $\frac{2}{5}$ | D. | $\frac{1}{2}$ |
11.△ABC与△DEF的相似比为1:4,则△ABC与△DEF的周长比为( )
| A. | 1:4 | B. | 1:3 | C. | 1:2 | D. | 1:16 |
8.如果( )×(-$\frac{2}{3}$)=-1,则括号内应填的数是( )
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | C-$\frac{2}{3}$ | D. | -$\frac{3}{2}$ |