题目内容
 如图,在以原点为圆心,2为半径的⊙O上有一点C,∠COA=45°,则C的坐标为( )
如图,在以原点为圆心,2为半径的⊙O上有一点C,∠COA=45°,则C的坐标为( )分析:作CB⊥OA于点B,根据半径为2,∠COA=45°确定点C的坐标即可;
解答: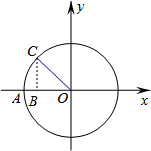 解:作CB⊥OA于点B,
解:作CB⊥OA于点B,
∵∠COA=45°,
∴三角形BCO为等腰直角三角形,
∵OA=2,
∴OB=BC=
,
又∵点C位于第二象限,
∴点C的坐标为:(-
,
),
故选C.
 解:作CB⊥OA于点B,
解:作CB⊥OA于点B,∵∠COA=45°,
∴三角形BCO为等腰直角三角形,
∵OA=2,
∴OB=BC=
| 2 |
又∵点C位于第二象限,
∴点C的坐标为:(-
| 2 |
| 2 |
故选C.
点评:本题考查了圆的认识,正确的构造直角三角形是解决此类题目的关键,注意点C所在的位置.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


 ,
,
 ,
,
