题目内容
如图⊙O内切于△ABC，切点分别为D、E、F；若∠ABC=40°，∠ACB=60°，连接OE、OF，则∠EOF为
- A.80°
- B.100°
- C.120°
- D.140°
B
分析：首先根据三角形的内角和定理，得∠A=80°，再根据切线的性质定理以及四边形的内角和定理，得∠EOF=100°．
解答：∵∠ABC=40°，∠ACB=60°，
∴∠A=80°，
∴∠EOF=180°-80°=100°．
故选B．
点评：此题要熟练运用切线的性质定理、四边形的内角和定理以及三角形的内角和定理．
分析：首先根据三角形的内角和定理，得∠A=80°，再根据切线的性质定理以及四边形的内角和定理，得∠EOF=100°．
解答：∵∠ABC=40°，∠ACB=60°，
∴∠A=80°，
∴∠EOF=180°-80°=100°．
故选B．
点评：此题要熟练运用切线的性质定理、四边形的内角和定理以及三角形的内角和定理．
练习册系列答案
阅读快车系列答案
相关题目
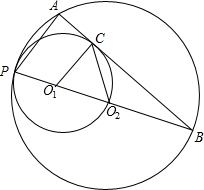接AB，过O1作O1C⊥BA于C，连接CO2．已知PA=
如图AOB是半径为1的单位圆的
（1998•大连）如图，⊙O1与⊙O2内切于点P．⊙O2的弦AB切⊙O1于点C，连接PA、PB，PC的延长线交⊙O2于点D．求证：（1）∠APC=∠BPC；
内接于⊙O，AB是⊙O的直径，延长AB到D，连结CD。请你结合图形，编写一道题。要求：再补充两个已知条件，并写出在所有已知条件下得出的一个结论。例如：
”