题目内容
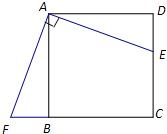已知：如图，在正方形ABCD中，点E在CD边上，点F在CB的延长线上，且FA⊥EA．求证：DE=BF．
证明：在正方形ABCD中，
AD=AB，
∠BAD=∠D=∠ABF=90°．
∵EA⊥AF，
∴∠BAE+∠DAE=∠BAF+∠BAE=90°
∴∠DAE=∠BAF
在△DAE和△BAF中，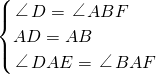
∴△DAE≌△BAF．
∴DE=BF．
分析：根据题中的条件，只要证明△DAE≌△BAF，再根据全等三角形的性质，不难论证DE=BF．
点评：解答本题时，主要用到了正方形的性质，全等三角形的判定以及全等三角形的性质．
AD=AB，
∠BAD=∠D=∠ABF=90°．
∵EA⊥AF，
∴∠BAE+∠DAE=∠BAF+∠BAE=90°
∴∠DAE=∠BAF
在△DAE和△BAF中，
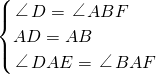
∴△DAE≌△BAF．
∴DE=BF．
分析：根据题中的条件，只要证明△DAE≌△BAF，再根据全等三角形的性质，不难论证DE=BF．
点评：解答本题时，主要用到了正方形的性质，全等三角形的判定以及全等三角形的性质．
练习册系列答案
阅读快车系列答案
相关题目
已知：如图，在正方形ABCD中，E是CB延长线上一点，EB=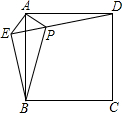
已知：如图，在正方形ABCD外取一点E，连接AE、BE、DE．过点A作AE的垂线交DE于点P．若AE=AP=1，PB=
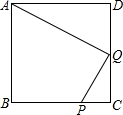已知：如图，在正方形ABCD中，P是BC上的点，且BP=3PC，Q是CD的中点．△ADQ与△QCP是否相似？
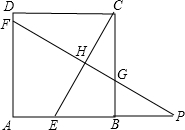、CE、CB于点F、H、G，交AB的延长线于点P．
已知：如图，在正方形ABCD中，E、F分别是AD、CD的中点．