题目内容
如图是小明设计利用光线来测量某古城墙CD高度的示意图,如果镜子P与古城墙的距离PD=12米,镜子P与小明的距离BP=1.5米,小明刚好从镜子中看到古城墙顶端点C,小明眼睛距地面的高度AB=1.2米,那么该古城墙的高度是( )
A.9.6米
B.18米
C.8米
D.24米
【答案】分析:由光学知识反射角等于入射角不难分析得出∠APB=∠CPD,再由∠ABP=∠CDP=90°得到△ABP∽△CDP,得到  代入数值求的CD的值即可.
代入数值求的CD的值即可.
解答:解:∵∠APB=∠CPD,∠ABP=∠CDP,
∴△ABP∽△CDP
∴ ,
,
即:
解得:CD=9.6米.
故选A.
点评:本题考查了直角三角形的有关知识,同时渗透光学中反射原理,注意到相似三角形,解决本题关键.
 代入数值求的CD的值即可.
代入数值求的CD的值即可.解答:解:∵∠APB=∠CPD,∠ABP=∠CDP,
∴△ABP∽△CDP
∴
 ,
,即:

解得:CD=9.6米.
故选A.
点评:本题考查了直角三角形的有关知识,同时渗透光学中反射原理,注意到相似三角形,解决本题关键.

练习册系列答案
相关题目
 如图是小明设计利用光线来测量某古城墙CD高度的示意图,如果镜子P与古城墙的距离PD=12米,镜子P与小明的距离BP=1.5米,小明刚好从镜子中看到古城墙顶端点C,小明眼睛距地面的高度AB=1.2米,那么该古城墙的高度是( )
如图是小明设计利用光线来测量某古城墙CD高度的示意图,如果镜子P与古城墙的距离PD=12米,镜子P与小明的距离BP=1.5米,小明刚好从镜子中看到古城墙顶端点C,小明眼睛距地面的高度AB=1.2米,那么该古城墙的高度是( )| A、9.6米 | B、18米 | C、8米 | D、24米 |
 9、如图是小明设计用手电来测量某古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是
9、如图是小明设计用手电来测量某古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是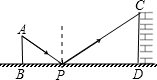 如图是小明设计用手电来测量某古城墙高度的示意图.点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是( )
如图是小明设计用手电来测量某古城墙高度的示意图.点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是( ) 如图是小明设计利用光线来测量某古城墙CD高度的示意图,如果镜子P与古城墙的距离PD=12米,镜子P与小明的距离BP=1.5米,小明刚好从镜子中看到古城墙顶端点C,小明眼睛距地面的高度AB=1.2米,那么该古城墙的高度是
如图是小明设计利用光线来测量某古城墙CD高度的示意图,如果镜子P与古城墙的距离PD=12米,镜子P与小明的距离BP=1.5米,小明刚好从镜子中看到古城墙顶端点C,小明眼睛距地面的高度AB=1.2米,那么该古城墙的高度是