Question

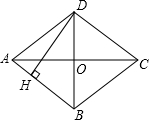如图，菱形ABCD对角线AC=8cm，BD=6cm，则菱形高DH长为（　　）

A．5cm

B．4.8cm

C．10cm

D．9.6cm

Answer 1

分析：根据菱形的对角线互相垂直平分求出OA、OB，然后利用勾股定理列式求出AB，再根据菱形的面积等于对角线乘积的一半和底乘以高两种方法列式计算即可得解．

解答：解：∵菱形ABCD对角线AC=8cm，BD=6cm，
∴AC⊥BD，
OA=

1

2

AC=

1

2

×8=4cm，
OB=

1

2

BD=

1

2

×6=3cm，
根据勾股定理，AB=

OA2+OB2

=

42+32

=5cm，
菱形ABCD的面积=

1

2

AC•BD=AB•DH，
即

1

2

×8×6=5DH，
解得DH=4.8cm．
故选B．

点评：本题考查了菱形的对角线互相垂直平分的性质，勾股定理的应用，根据菱形的面积的两个求解方法列出方程是解题的关键．