题目内容
 在直角坐标系xoy中,一次函数
在直角坐标系xoy中,一次函数 的图象与x轴、y轴分别交于点B和点A,点C的坐标是(0,1),点D在y轴上且满足∠BCD=∠ABD.求D点的坐标.
的图象与x轴、y轴分别交于点B和点A,点C的坐标是(0,1),点D在y轴上且满足∠BCD=∠ABD.求D点的坐标.
解:∵A、B是直线与y轴、x轴的交点,
令y=0,解得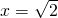 ,
,
∴ ;
;
令x=0,解得y=-3,
∴A(0,-3);
由勾股定理得, ,
,
(1)若D点在C点上方时,则∠BCD为钝角,
∵∠BCD=∠ABD,又∠CDB=∠ADB,
∴△BCD∽△ABD,
∴ ,
,
设D(0,y),则y>1,
∵ ,
,
∴ ,
,
∴8y2-22y+5=0,
解得 或
或 (舍去),
(舍去),
∴点D的坐标为(0, ),
),
(2)若D点在AC之间时,则∠BCD为锐角,
∵∠ABD=∠BCD,又∠BAD=∠CAB,
∴△ABD∽△ACB,∴ ,
,
设D(0,y),则-3<y<1,又 ,
,
∴ ,
,
整理得8y2-18y-5=0,
解得 或
或 (舍去),
(舍去),
∴D点坐标为(0,- );
);
(3)若D点在A点下方时,有∠BAC=∠ABD+∠ADB>∠ABD,
又显然∠BAC<∠BCD,
∴D点在A点下方是不可能的.
综上所述,D点的坐标为(0, )或(0,-
)或(0,- ).
).
分析:先根据一次函数的解析式求出点A及点B的坐标,利用勾股定理解出线段BC、AB的坐标,分一下三种情况进行讨论,(1)若D点在C点上方时,(2)若D点在AC之间时,(3)若D点在A点下方时,每一种情况下求出点D的坐标即可.
点评:此题考查了一次函数的综合应用及坐标与图形的性质,综合性较强,解答本题容易出错的地方时遗漏点D的位置,难点在于每一种情况下求出点D的坐标,难度较大.
令y=0,解得
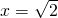 ,
,∴
 ;
;令x=0,解得y=-3,
∴A(0,-3);
由勾股定理得,
 ,
,(1)若D点在C点上方时,则∠BCD为钝角,
∵∠BCD=∠ABD,又∠CDB=∠ADB,
∴△BCD∽△ABD,
∴
 ,
,设D(0,y),则y>1,
∵
 ,
,∴
 ,
,∴8y2-22y+5=0,
解得
 或
或 (舍去),
(舍去),∴点D的坐标为(0,
 ),
),(2)若D点在AC之间时,则∠BCD为锐角,
∵∠ABD=∠BCD,又∠BAD=∠CAB,
∴△ABD∽△ACB,∴
 ,
,设D(0,y),则-3<y<1,又
 ,
,∴
 ,
,整理得8y2-18y-5=0,
解得
 或
或 (舍去),
(舍去),∴D点坐标为(0,-
 );
);(3)若D点在A点下方时,有∠BAC=∠ABD+∠ADB>∠ABD,
又显然∠BAC<∠BCD,
∴D点在A点下方是不可能的.
综上所述,D点的坐标为(0,
 )或(0,-
)或(0,- ).
).分析:先根据一次函数的解析式求出点A及点B的坐标,利用勾股定理解出线段BC、AB的坐标,分一下三种情况进行讨论,(1)若D点在C点上方时,(2)若D点在AC之间时,(3)若D点在A点下方时,每一种情况下求出点D的坐标即可.
点评:此题考查了一次函数的综合应用及坐标与图形的性质,综合性较强,解答本题容易出错的地方时遗漏点D的位置,难点在于每一种情况下求出点D的坐标,难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

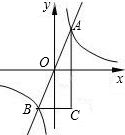 在直角坐标系xoy中,函数y=4x的图象与反比例函数y=
在直角坐标系xoy中,函数y=4x的图象与反比例函数y= (2012•北京二模)已知:如图,在直角坐标系xOy中,点A(8,0)、B(0,6),点C在x轴的负半轴上,AB=AC.动点M在x轴上从点C向点A移动,动点N在线段AB上从点A向点B移动,点M、N同时出发,且移动的速度都为每秒1个单位,移动时间为t秒(0<t<10).
(2012•北京二模)已知:如图,在直角坐标系xOy中,点A(8,0)、B(0,6),点C在x轴的负半轴上,AB=AC.动点M在x轴上从点C向点A移动,动点N在线段AB上从点A向点B移动,点M、N同时出发,且移动的速度都为每秒1个单位,移动时间为t秒(0<t<10). 析式为y=x2-mx+n.方程x2-mx+n=0的两根倒数和为-4.
析式为y=x2-mx+n.方程x2-mx+n=0的两根倒数和为-4.