Question

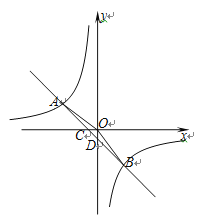
【题目】如图，在平面直角坐标系中，一次函数的图象与反比例函数的图象交于第二、四象限内的A，B两点，与x轴交于点C，与y轴交于点D，点B的坐标是（m，﹣4），连接AO，AO=5，sin∠AOC=．

（1）求反比例函数的解析式

（2）连接OB，求△AOB的面积

(3) 根据图象直接写出当时，x的取值范围．

Answer 1

【答案】（1） ；（2） ；(3)

【解析】

（1）过点A作AE⊥x轴于点E，设反比例函数解析式为y=．通过解直角三角形求出线段AE、OE的长度，即求出点A的坐标，再由点A的坐标利用待定系数法求出反比例函数解析式即可；

（2）由点B在反比例函数图象上可求出点B的坐标，设直线AB的解析式为y=ax+b，由点A、B的坐标利用待定系数法求出直线AB的解析式，令该解析式中y=0即可求出点C的坐标，再利用三角形的面积公式即可得出结论；

（3）观察图象可得x的取值范围.

(1)过点A作AE⊥x轴于点E，

设反比例函数的解析式为，

∵AE⊥x，

∴∠AEO=90°，

在Rt△AEO中，AO=5，sin∠AOC=，

∴AE=3，OE=4，

∴A(-4,3)，

∵点A在反比例函数上，

∴k=-12，

；

(2)∵B（m，-4）在反比例函数图象上，

∴，

，

∴B（3，-4）设直线AB的解析式为，

将点A(-4,3), B（3，-4）代入，

得，

解得，

∴一次函数解析式为，

令中，

解得：，

∴C（-1,0），

∴，

（3）由图象可得：