题目内容
【题目】从三角形
不是等腰三角形
一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原三角形相似，我们把这条线段叫做这个三角形的完美分割线．
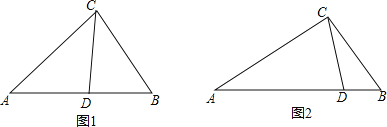
如图1，在
中，CD为角平分线，
，
，求证：CD为的完美分割线．
在中，
，CD是的完美分割线，且
为等腰三角形，求
的度数．
如图2，中，
，
，CD是的完美分割线，且是以CD为底边的等腰三角形，求完美分割线CD的长．
【答案】（1）见解析；（2）
或
；（3）
．
【解析】
根据完美分割线的定义只要证明
不是等腰三角形，
是等腰三角形，
∽
即可．
分三种情形讨论即可
如图2，当
时，
如图3中，当
时，
如图4中，当
时，分别求出
即可．
设
，利用
∽
，得
，列出方程即可解决问题．
解：如图1中，
，
，
，
不是等腰三角形，
平分，
，
，
为等腰三角形，
，
，
∽，
是
的完美分割线．
当时，如图2，
，
∽，
，
．
当时，如图3中，
，
∽，
，
．
当时，如图4中，
，
∽，
，
，矛盾，舍弃．
或．
由已知
，
∽，
，设，
，
，
，
∽，
，
．
练习册系列答案
相关题目
