题目内容
7. 如图,在直角坐标系中有正方形OABC,以OA为直径作⊙M,在半圆上有一动点P,连接PO、PA、PB、PC,已知A(4,0).
如图,在直角坐标系中有正方形OABC,以OA为直径作⊙M,在半圆上有一动点P,连接PO、PA、PB、PC,已知A(4,0).(1)OP=2时,P点的坐标是(1,$\sqrt{3}$);
(2)求当OP为多少时,△OPC为等腰三角形;
(3)设P(a,b),S△POC=S1,S△POA=S2,S△PAB=S3,求出S=2S1S3-S22的最大值,并求出此时P的坐标.
分析 (1)根据正方形的性质求出OA=AB=BC=CO=4,根据圆周角定理得到∠OPA=90°,根据勾股定理求出OE、PE,得到答案;
(2)分PC=PO、CO=CP两种情况,根据等腰三角形的性质以及勾股定理计算即可;
(3)用a、b分别表示出S1、S2、S3,根据射影定理求出b2=a(4-a),根据二次函数的性质解答即可.
解答 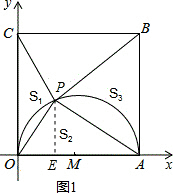 解:(1)∵点A的坐标为(4,0),
解:(1)∵点A的坐标为(4,0),
∴OA=4,
∵四边形OABC为正方形,
∴OA=AB=BC=CO=4,
∵OA为⊙M的直径,
∴∠OPA=90°,OP=2,OA=4,
∴∠OAP=30°,
∴∠OPE=30°,又OP=2,
∴OE=1,PE=$\sqrt{3}$,
∴P(1,$\sqrt{3}$);
(2)如图2,当PC=PO时此时P位于四边形OABC的中心,
过点P作PE⊥OA于E,作PF⊥OC于F,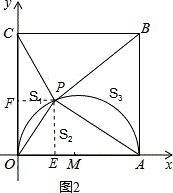
则四边形OEPF是正方形,
∴PE=OE=$\frac{1}{2}$OA=2,
∴OP=2$\sqrt{2}$,
如图3,当CO=CP时,以点C为圆心,CO为半径作圆与弧OA的交点为点P.
连PO,连接PM,CM,CM交OP于点G,
在△ADO和△PDO中,
$\left\{\begin{array}{l}{CO=CP}\\{MO=MP}\\{CM=CM}\end{array}\right.$,
∴△ADO≌△PDO,
∴CM⊥OP,OG=PG,
∵OC=4,OM=2,
∴CM=2$\sqrt{5}$,
∴OG=$\frac{4×2}{2\sqrt{5}}$=$\frac{4\sqrt{5}}{5}$,
则OP=2OG=$\frac{8\sqrt{5}}{5}$,
当OP为2$\sqrt{2}$或$\frac{8\sqrt{5}}{5}$时,△OPC为等腰三角形;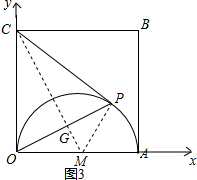
(3)∵P(a,b),OA=AB=CO=4,
∴S1=2a,S3=8-2a,b2=4a-a2,S2=2b,
如图2,P(a,b),
由射影定理得,PE2=OE•AE,即b2=a(4-a),
∴S=2×2a×(8-2a)-(2b)2=8(4a-a2)-4b2=-4(a-2)2+16,
当a=2时,S最大=16,
当a=2时,b=$\sqrt{a(4-a)}$=2,
∴P的坐标为(2,2).
点评 本题考查的是圆周角定理、全等三角形的判定和性质、正方形的性质、二次函数的解析式的求法以及二次函数的性质的综合运用,灵活运用相关的定理、正确作出辅助线是解题的关键.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案 如图,△ABC中,D为AB的中点,DE∥BC,则下列结论中错误的是( )
如图,△ABC中,D为AB的中点,DE∥BC,则下列结论中错误的是( )| A. | $\frac{AD}{BD}=\frac{DE}{BC}$ | B. | $\frac{AD}{BD}=\frac{AE}{EC}$ | ||
| C. | DE=$\frac{1}{2}$BC | D. | S△ADE=$\frac{1}{3}$S四边形BCED |
 如图,点A,D是网格中的两点,现在将点A进行两次平移,第一次平移后的对应点为B第二次平移后的对应点为C,顺次连接ABCD四点,恰好是一个等腰梯形,请你在网格中画出图形,使这个等腰梯形的面积为12.
如图,点A,D是网格中的两点,现在将点A进行两次平移,第一次平移后的对应点为B第二次平移后的对应点为C,顺次连接ABCD四点,恰好是一个等腰梯形,请你在网格中画出图形,使这个等腰梯形的面积为12.  由于现在人们生活水平的普遍提高,大家对自己的生存环境越来越关注,特别是对大气环境质量的关注,而空气中又以PM2.5对人体的危害性最大,某市环保局对该市市民进行了一项民意调查,以了解PM2.5浓度升高时对人们户外活动是否有影响,并制作了统计图表的一部分如下:
由于现在人们生活水平的普遍提高,大家对自己的生存环境越来越关注,特别是对大气环境质量的关注,而空气中又以PM2.5对人体的危害性最大,某市环保局对该市市民进行了一项民意调查,以了解PM2.5浓度升高时对人们户外活动是否有影响,并制作了统计图表的一部分如下:| 公众对于户外活动的态度 | 百分比 |
| A.没有影响 | a |
| B.影响不大,还可以进行户外活动 | 5% |
| C.有影响,减少户外活动 | 42% |
| D.影响很大,尽可能不去户外活动 | b |
| E.不关心这个问题 | 6% |
(2)根据以上信息,请直接补全条形统计图;
(3)若该市约400万人,根据上述信息,请你估计一下持有“影响很大,尽可能不去户外活动”这种态度的约有多少万人.(说明:“PM2.5”是指大气中危害健康的直径小于2.5微米的颗粒物,也称可入肺颗粒物)
 如图,已知直线y=4-x与反比例函数y=$\frac{m}{x}$(m>0,x>0)的图象交于A,B两点,且点A的横坐标为1,与x轴,y轴分别相交于C,D两点.
如图,已知直线y=4-x与反比例函数y=$\frac{m}{x}$(m>0,x>0)的图象交于A,B两点,且点A的横坐标为1,与x轴,y轴分别相交于C,D两点. 如图,矩形ACBE中,AC=6,BC=8,D是AB上一动点,当AD=$\frac{11}{5}$时,∠BDC=2∠BAE.
如图,矩形ACBE中,AC=6,BC=8,D是AB上一动点,当AD=$\frac{11}{5}$时,∠BDC=2∠BAE. 如图,二次函数y=-$\frac{1}{{m}^{2}}$x2-$\frac{2x}{m}$+3(其中m是常数,且m>0)的图象与x轴交于A、B(点A位于点B的左侧),与y轴交于点C,作CD∥AB,点D在二次函数的图象上,连接BD,过点B作射线BE交二次函数的图象于点E,使得AB平分∠DBE.
如图,二次函数y=-$\frac{1}{{m}^{2}}$x2-$\frac{2x}{m}$+3(其中m是常数,且m>0)的图象与x轴交于A、B(点A位于点B的左侧),与y轴交于点C,作CD∥AB,点D在二次函数的图象上,连接BD,过点B作射线BE交二次函数的图象于点E,使得AB平分∠DBE. 如图,已知AE=CF,AD∥BC,AD=BC.求证:
如图,已知AE=CF,AD∥BC,AD=BC.求证: 如图,在矩形ABCD中,AD=$\sqrt{2}$AB,AE平分∠BAD,DF⊥AE于F,BF交DE、CD于O、H,下列结论:①∠DEA=∠DEC;②BF=FH;③OE=OD;④BC-CH=2EF;⑤AB=HF,其中正确结论的个数是( )
如图,在矩形ABCD中,AD=$\sqrt{2}$AB,AE平分∠BAD,DF⊥AE于F,BF交DE、CD于O、H,下列结论:①∠DEA=∠DEC;②BF=FH;③OE=OD;④BC-CH=2EF;⑤AB=HF,其中正确结论的个数是( )