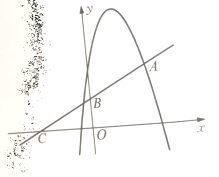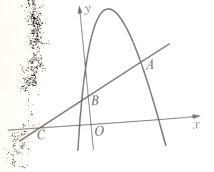题目内容
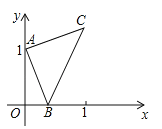
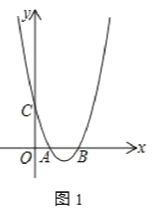
【题目】已知二次函数y=x2+bx+c,其图象抛物线交x轴于点A(1,0)、B(3,0),交 y轴于点C,直线l过点C,且交抛物线于另一点E(点E不与点A、B重合).
(1)直接写出二次函数的解析式;
(2)若直线l1经过抛物线顶点D,交x轴于点F,且l1∥l,则以点C、D、E、F为顶点的四边形能否为平行四边形,若能,求出点E的坐标;若不能,请说明理由;
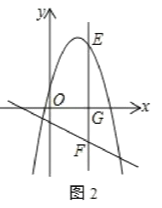
(3)将此抛物线沿着y=2翻折,E为所得新抛物线x轴上方一动点,过E作x轴的垂线,交x轴于G,交直线y=-![]() x-1于点F,求
x-1于点F,求![]() 的最大值.
的最大值.
【答案】(1) y=x2-4x+3;(2)能,点E (2+![]() ,2)、(2-
,2)、(2-![]() ,2)、(2+
,2)、(2+![]() ,4)、(2-
,4)、(2-![]() ,4); (3)
,4); (3) ![]()
【解析】
(1)用抛物线交点式表达式,即可求解;
(2)分当![]() 为平行四边形的对角线、平行四边形的一条边,两种情况求解即可;
为平行四边形的对角线、平行四边形的一条边,两种情况求解即可;
(3)根据题意求出新抛物线的表达式,再将点E和点F坐标表示出来,可得 ,即可求解.
,即可求解.
解:(1)用抛物线交点式表达式得:
抛物线的表达式为:![]() ;
;
(2)能,理由:
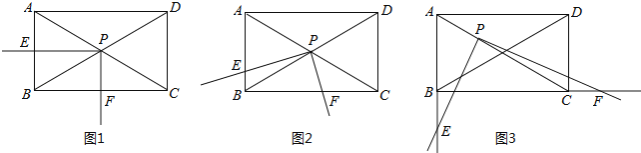
①当![]() 为平行四边形的对角线时,如下图,
为平行四边形的对角线时,如下图,
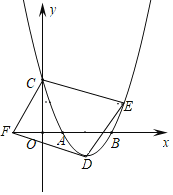
设点![]() 的坐标为
的坐标为![]() ,
,
则![]() 中点的坐标为
中点的坐标为![]() ,该点也为
,该点也为![]() 的中点
的中点
即:![]() ,解得:
,解得:![]() ,
,
故点![]() 的坐标为
的坐标为![]() ,
,![]() 或
或![]() ,
,![]() ;
;
②当![]() 为平行四边形的一条边时,如下图,
为平行四边形的一条边时,如下图,
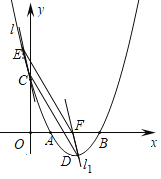
设点![]() 坐标为
坐标为![]() ,
,
点![]() 向左平移2个单位、向上平移4个单位,得到点
向左平移2个单位、向上平移4个单位,得到点![]() ,
,
同样点![]() 向左平移2个单位、向上平移4个单位,得到点
向左平移2个单位、向上平移4个单位,得到点![]() ,
,
将点![]() 坐标代入二次函数表达式并解得:
坐标代入二次函数表达式并解得:![]() ,
,
则点![]() ,
,![]() 或
或![]() ,
,![]() ;
;
故点![]() 的坐标为
的坐标为![]() ,
,![]() 或
或![]() ,
,![]() 或
或![]() ,
,![]() 或
或![]() ,
,![]() ;
;
(3)抛物线沿着![]() 翻折后,顶点坐标为
翻折后,顶点坐标为![]() ,
,
则新抛物线的表达式为:![]() ,
,
设点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() ,
,
则 ,
,
即:![]() 的最大值为:
的最大值为:![]() .
.

 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案【题目】某公司共有![]() 三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图.
三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图.

各部门人数及每人所创年利润统计表
部门 | 员工人数 | 每人所创的年利润/万元 |
A | 5 | 10 |
B |
| 8 |
C |
| 5 |
(1)①在扇形图中,C部门所对应的圆心角的度数为___________;
②在统计表中,![]() ___________,
___________,![]() ___________;
___________;
(2)求这个公司平均每人所创年利润.
【题目】随着互联网、移动终端的迅速发展,数字化阅读越来越普及,公交、地铁上的“低头族”越来越多,某研究机构针对“您如何看待数字化阅读”问题进行了随机问卷调查(问卷调查表如下图所示),并将调查结果绘制成图①和图②所示的统计图(均不完整).
“您如何看待数字化阅读”问卷调查表
您好!这是一份关于“您如何看待数字化阅读问卷调查表,请在表格中选择一项您最认同的观点,在其后空格内打“√”,非常感谢您的合作.
代码 | 观点 | |
| 获取信息方便,可以随时随地观看 | |
| 价格便宜易得 | |
| 使得人们成为“低头族”,不利于人际交往 | |
| 内容丰富,比纸质书涉猎更广 | |
| 其他 | |
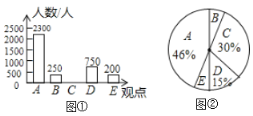
请根据统计图中提供的信息,解答下列问题:
(I)本次接受调查的总人数是__________人,并将条形统计图补充完整.
(Ⅱ)在扇形统计图中,观点![]() 的百分比是___________,表示观点
的百分比是___________,表示观点![]() 的扇形的圆心角度数为_________度.
的扇形的圆心角度数为_________度.
(Ⅲ)某市共有![]() 万人,请根据以上调查结果估算该市持
万人,请根据以上调查结果估算该市持![]() ,
,![]() ,
,![]() 观点赞成数字化阅读的人数共有多少万人.
观点赞成数字化阅读的人数共有多少万人.