题目内容
在边长为1的正方形ABCD中,以点A为圆心,AB为半径作圆,E是BC边上的一个动点(不运动至B,C),过点E作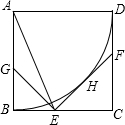 弧BD的切线EF,交CD于F,H是切点,过点E作EG⊥EF,交AB于点G,连接AE.
弧BD的切线EF,交CD于F,H是切点,过点E作EG⊥EF,交AB于点G,连接AE.(1)求证:△AGE是等腰三角形;
(2)设BE=x,△BGE与△CEF的面积比
| S△BGE | S△CEF |
(3)在BC边上(点B、C除外)是否存在一点E,使得GE=EF,若存在,求出此时BE的长,若不存在,请说明理由.
分析:(1)如图连AH,根据切线的性质可以得到AH⊥EF,而GE⊥EF,由此得到GE∥AH,所以∠GEA=∠EAH,又根据已知条件可以证明△AHE≌△ABE,由此得到∠BAE=∠EAH,进一步得到∠BAE=∠GEA,从而证明AE=EG,即△AGE是等腰三角形;
(2)设EH=EB=x,可以用x分别表示EC,CF=1-FD,根据切线长定理知道FD=FH,由此得到EF=EH+HF=x+FD,而在Rt△ECF中,EF2=EC2+CF2,可以得到(1-x)2+(1-FD)2=(x+FD)2,由此可以把DF也用x表示,又根据已知条件容易证明△GEB∽△EFC,根据相似三角形的性质得到
=
,而
=
=
•
=(
)2={
}2=
(1+x)2,这样就求出y关于x的函数关系式;
(3)假设BC上存在一点E,能使GE=EF,则
=
=1,根据(2)可以得到x=
,解此方程求出x,然后结合已知条件就可以判断E点是否存在.
(2)设EH=EB=x,可以用x分别表示EC,CF=1-FD,根据切线长定理知道FD=FH,由此得到EF=EH+HF=x+FD,而在Rt△ECF中,EF2=EC2+CF2,可以得到(1-x)2+(1-FD)2=(x+FD)2,由此可以把DF也用x表示,又根据已知条件容易证明△GEB∽△EFC,根据相似三角形的性质得到
| BE |
| CF |
| BG |
| EC |
| S△BGE |
| S△CEF |
| ||
|
| BE |
| CF |
| BG |
| EC |
| BE |
| CF |
| x | ||
|
| 1 |
| 4 |
(3)假设BC上存在一点E,能使GE=EF,则
| GE |
| EF |
| BE |
| CF |
| 2x |
| 1+x |
解答: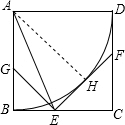 解:(1)连AH,
解:(1)连AH,
∵AH⊥EF,GE⊥EF,
∴GE∥AH,
∴∠GEA=∠EAH,
∵AH=AB,AE=AE,∠ABE=∠AHB,
∴△AHE≌△ABE,
∴∠BAE=∠EAH,
∴∠BAE=∠GEA,
∴AG=EG,即△AGE是等腰三角形.
(2)∵EH=EB=x,
∴EC=1-x,CF=1-FD,
∵FD=FH,
∴EF=EH+HF=x+FD,
在Rt△ECF中,EF2=EC2+CF2,
∴(1-x)2+(1-FD)2=(x+FD)2,整理得,(1+x)FD=1-x,
∴FD=
CF=1-FD=1-
=
,
∵∠B=∠C,
又GE⊥EF,
∴∠GEB=∠FEC,
∴△GEB∽△EFC,
∴
=
,
∴
=
=
•
=(
)2={
}2=
(1+x)2,
∴y=
x2+
x+
(0<x<1).
(3)假设BC上存在一点E,能使GE=EF,
则
=
=1,
∴x=
,解得x=0或x=1,经检验x=0或x=1是原方程的解但动点E不能与B,C点重合,
故x≠0且x≠1,
∴BC边上符合条件的E点不存在.
 解:(1)连AH,
解:(1)连AH,∵AH⊥EF,GE⊥EF,
∴GE∥AH,
∴∠GEA=∠EAH,
∵AH=AB,AE=AE,∠ABE=∠AHB,
∴△AHE≌△ABE,
∴∠BAE=∠EAH,
∴∠BAE=∠GEA,
∴AG=EG,即△AGE是等腰三角形.
(2)∵EH=EB=x,
∴EC=1-x,CF=1-FD,
∵FD=FH,
∴EF=EH+HF=x+FD,
在Rt△ECF中,EF2=EC2+CF2,
∴(1-x)2+(1-FD)2=(x+FD)2,整理得,(1+x)FD=1-x,
∴FD=
| 1-x |
| 1+x |
| 1-x |
| 1+x |
| 2x |
| 1+x |
∵∠B=∠C,
又GE⊥EF,
∴∠GEB=∠FEC,
∴△GEB∽△EFC,
∴
| BE |
| CF |
| BG |
| EC |
∴
| S△BGE |
| S△CEF |
| ||
|
| BE |
| CF |
| BG |
| EC |
| BE |
| CF |
| x | ||
|
| 1 |
| 4 |
∴y=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
(3)假设BC上存在一点E,能使GE=EF,
则
| GE |
| EF |
| BE |
| CF |
∴x=
| 2x |
| 1+x |
故x≠0且x≠1,
∴BC边上符合条件的E点不存在.
点评:此题把圆的知识放在正方形的背景中,然后把等腰三角形,相似三角形,求函数关系式及自变量与函数值等知识结合起来,综合性很强,学生要有比较好的解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
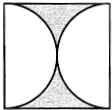 如图,在边长为a的正方形铁块中,以两对边中点为圆心,以a为直径截取两个半圆,求余下废料的面积是多少?
如图,在边长为a的正方形铁块中,以两对边中点为圆心,以a为直径截取两个半圆,求余下废料的面积是多少?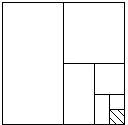 我国著名的数学家华罗庚曾说过:“数形结合百般好,割裂分家万事非”,如图,在边长为1的正方形纸板上,依次贴上面积为
我国著名的数学家华罗庚曾说过:“数形结合百般好,割裂分家万事非”,如图,在边长为1的正方形纸板上,依次贴上面积为
 在边长为16cm的正方形纸片的四个角各剪去一个同样大小的正方形,折成一个无盖的长方体.
在边长为16cm的正方形纸片的四个角各剪去一个同样大小的正方形,折成一个无盖的长方体.