题目内容
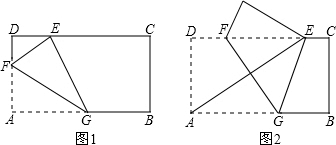
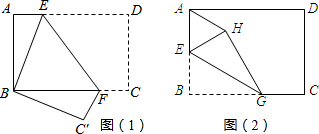
 已知矩形纸片ABCD中,AB=1,BC=2.将该纸片折叠成一个平面图形,折痕EF不经过A点(E,F是该矩形边界上的点),折叠后点A落在点A′处,给出以下判断:
已知矩形纸片ABCD中,AB=1,BC=2.将该纸片折叠成一个平面图形,折痕EF不经过A点(E,F是该矩形边界上的点),折叠后点A落在点A′处,给出以下判断:
①当四边形A′CDF为正方形时,EF= ;
;
②当EF= 时,四边形A′CDF为正方形;
时,四边形A′CDF为正方形;
③当EF= 时,四边形BA′CD为等腰梯形;
时,四边形BA′CD为等腰梯形;
④当四边形BA′CD为等腰梯形时,EF= .
.
其中正确的是________(把所有正确结论的序号都填在横线上).
①③④
分析:①根据正方形的性质和矩形的性质判定“A'F刚好是矩形ABCD的中位线点E和点B重合,EF即正方形ABA'F的对角线”,所以在直角△AEF中,由勾股定理可以求得EF= ;
;
②根据①中的EF= 可以推知,当EF沿着BC边平移时,EF的长度不变,但是四边形A′CDF不是正方形;
可以推知,当EF沿着BC边平移时,EF的长度不变,但是四边形A′CDF不是正方形;
③根据勾股定理求得BD= ,所以由已知条件可以推知EF与对角线BD重合.由折叠的性质、矩形的性质易证四边形BA′CD为等腰梯形;
,所以由已知条件可以推知EF与对角线BD重合.由折叠的性质、矩形的性质易证四边形BA′CD为等腰梯形;
④当四边形BA′CD为等腰梯形时,EF与对角线BD重合,即EF= .
.
解答: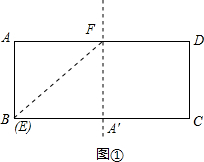 解:∵在矩形纸片ABCD中,AB=1,BC=2,
解:∵在矩形纸片ABCD中,AB=1,BC=2,
∴BC=2AB.
①如图①.∵A'CDF为正方形,说明A'F刚好是矩形ABCD的中位线,
∴AF=BA'=1,即点E和点B重合,EF即正方形ABA'F的对角线.
EF= AB=
AB= .
.
故①正确;.
②如图①,由①知四边形A′CDF为正方形时,EF= ,此时点E与点B重合.
,此时点E与点B重合.
EF可以沿着BC边平移,当点E与点B不重合时,四边形A′CDF就不是正方形.
故②错误;
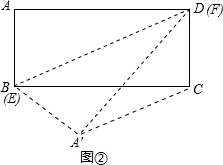
③如图②,∵BD= =
= =
= ,EF=
,EF= ,
,
∴BD=EF,
∴EF与对角线BD重合.
易证BA'CD是等腰梯形.
故③正确;
④BA'CD为等腰梯形,只能是BA'=CD,EF与BD重合,所以EF= .
.
故④正确.
综上所述,正确的是①③④.
故填:①③④.
点评:本题考查了折叠的性质.折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
分析:①根据正方形的性质和矩形的性质判定“A'F刚好是矩形ABCD的中位线点E和点B重合,EF即正方形ABA'F的对角线”,所以在直角△AEF中,由勾股定理可以求得EF=
 ;
;②根据①中的EF=
 可以推知,当EF沿着BC边平移时,EF的长度不变,但是四边形A′CDF不是正方形;
可以推知,当EF沿着BC边平移时,EF的长度不变,但是四边形A′CDF不是正方形;③根据勾股定理求得BD=
 ,所以由已知条件可以推知EF与对角线BD重合.由折叠的性质、矩形的性质易证四边形BA′CD为等腰梯形;
,所以由已知条件可以推知EF与对角线BD重合.由折叠的性质、矩形的性质易证四边形BA′CD为等腰梯形;④当四边形BA′CD为等腰梯形时,EF与对角线BD重合,即EF=
 .
.解答:
 解:∵在矩形纸片ABCD中,AB=1,BC=2,
解:∵在矩形纸片ABCD中,AB=1,BC=2,∴BC=2AB.
①如图①.∵A'CDF为正方形,说明A'F刚好是矩形ABCD的中位线,
∴AF=BA'=1,即点E和点B重合,EF即正方形ABA'F的对角线.
EF=
 AB=
AB= .
.故①正确;.
②如图①,由①知四边形A′CDF为正方形时,EF=
 ,此时点E与点B重合.
,此时点E与点B重合.EF可以沿着BC边平移,当点E与点B不重合时,四边形A′CDF就不是正方形.
故②错误;

③如图②,∵BD=
 =
= =
= ,EF=
,EF= ,
,∴BD=EF,
∴EF与对角线BD重合.
易证BA'CD是等腰梯形.
故③正确;
④BA'CD为等腰梯形,只能是BA'=CD,EF与BD重合,所以EF=
 .
.故④正确.
综上所述,正确的是①③④.
故填:①③④.
点评:本题考查了折叠的性质.折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
相关题目
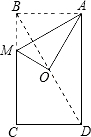 如图,已知矩形纸片ABCD中,AD=6,AB=a(a<6),在BC边上取一点M,将△ABM沿AM折叠后点B恰好落在矩形ABCD的对称中心O处,则a的值为
如图,已知矩形纸片ABCD中,AD=6,AB=a(a<6),在BC边上取一点M,将△ABM沿AM折叠后点B恰好落在矩形ABCD的对称中心O处,则a的值为