Question

【题目】平面直角坐标系xOy中，对于任意的三个点A、B、C，给出如下定义：若矩形的任何一条边均与某条坐标轴平行，且A，B，C三点都在矩形的内部或边界上，则称该矩形为点A，B，C的“三点矩形”．在点A，B，C的所有“三点矩形”中，若存在面积最小的矩形，则称该矩形为点A，B，C的“迷你三点矩形”．

如图1，矩形DEFG，矩形IJCH都是点A，B，C的“三点矩形”，矩形IJCH是点A，B，C的“迷你三点矩形”．

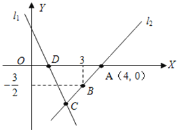
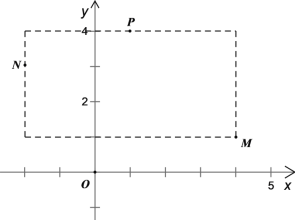
如图2，已知M(4，1)，N(-2，3)，点P(m，n)．

（1）①若m＝1，n＝4，则点M，N，P的“迷你三点矩形”的周长为 ，面积为 ；

②若m＝1，点M，N，P的“迷你三点矩形”的面积为24，求n的值；

（2）若点P在直线y＝-2x＋4上．当点M，N，P的“迷你三点矩形”为正方形时，直接写出点P的坐标．

Answer 1

【答案】（1）①18，18；②n的值为5或；（2）点P的坐标为或．

【解析】

（1）①根据“迷你三点矩形”的定义画出图形，再根据矩形的周长和面积公式求解即可；

②先根据点M、N的坐标可得“迷你三点矩形”的一条边的长，再根据矩形的面积公式可得另一条边的长，由此即可得；

（2）先根据“迷你三点矩形”的定义可得正方形的边长，从而可得点P的纵坐标，再代入直线求解即可得．

（1）①如图，画出点M、N、P的“迷你三点矩形”

则矩形的两边的长分别为，

因此，矩形的周长为，面积为

故答案为：18，18；

②

点M，N，P的“迷你三点矩形”的一条边的长为

又点M，N，P的“迷你三点矩形”的面积为24，且点M、N的纵坐标之差为

点M，N，P的“迷你三点矩形”的另一条边的长为，且点P的纵坐标大于点N的纵坐标或小于点M的纵坐标

则有或

解得或

故n的值为5或；

（2）由②知，点M，N，P的“迷你三点矩形”的一条边的长为

则点M，N，P的“迷你三点矩形”为正方形时，正方形的边长为6

同②的方法可得：或

解得或

点在直线上

当时，，解得

当时，，解得

则点P的坐标为或．