��Ŀ����
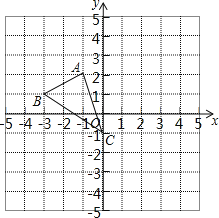
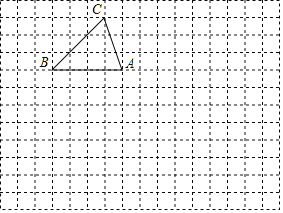
����Ŀ������ͼ��ʾ�������������У�ÿ��С�����εı߳���Ϊ1����ABC�Ķ��㶼�ڸ���ϣ������ߵĽ��㣩��
��1��������ͼ��ʾ������ƽ���ڽ����ʵ���ƽ��ֱ������ϵ��ʹ��A����Ϊ����1��2������B������Ϊ����5��2����������ֱ������ϵ��
��2����C������Ϊ���� ������ ������ֱ��д�������
��3������ABC������ƽ��6����λ��õ���Ӧ����A1B1C1���ٽ���A1B1C1��y�ᷭ������A2B2C2��
����������ϵ�л�����A2B2C2��
������P��m��n������ABC��������һ�㣬P2����A2B2C2������P��Ӧ�ĵ㣬д����P2������Ϊ���� ������ ��������ֱ��д�������
������y������һ��Q��ʹ�õ�Q��A2��C2����ľ���֮����С����ʱ��QA2+QC2�ij���֮����СֵΪ�� ��������ͼ�л�����Q��λ�ã���ֱ��д����Сֵ�𰸣�
���𰸡���1������������2������2��5������3���ټ��������ڵ�P2������Ϊ����m��n��6������3![]()
��������
��1�������ʵ���ƽ��ֱ������ϵ�����ݵ�A����Ϊ����1��2������B������Ϊ����5��2�����ɻ���ֱ������ϵ��
��2����������ϵ����д����C�����ꣻ
��3������ABC������ƽ��6����λ��õ���Ӧ����A1B1C1���ٽ���A1B1C1��y�ᷭ������A2B2C2��
�ټ���������ϵ�л�����A2B2C2��
������P��m��n������ABC��������һ�㣬P2����A2B2C2������P��Ӧ�ĵ㣬����д����P2�����ꣻ
�۸��ݶԳ��Լ�����y������һ��Q��ʹ�õ�Q��A2��C2����ľ���֮����С�������������QA2+QC2�ij���֮����Сֵ��
��1���ߵ�A����Ϊ����1��2������B������Ϊ����5��2����

��ͼ��ʾ����Ϊ��������ֱ������ϵ��
��2����������ϵ��֪��
��C����������2��5����
�ʴ�Ϊ����2��5��
��3������ABC������ƽ��6����λ��õ���Ӧ����A1B1C1��
�ٽ���A1B1C1��y�ᷭ������A2B2C2��
����ͼ��Ϊ����ϵ�л�������A2B2C2��

�ڵ�P��m��n������ABC��������һ�㣬
P2����A2B2C2������P��Ӧ�ĵ㣬
���P2����������m��n��6����
�ʴ�Ϊ����m��n��6��
�۸��ݶԳ��Կ�֪��
��y������һ��Q��ʹ�õ�Q��A2��C2����ľ���֮����С��
������A2C1��y���ڵ�Q����ʱQA2+QC2�ij���֮����С��

��ΪA2C1�ij���A2C1��3![]() ��
��
��QA2+QC2�ij���֮����СֵΪ3![]() ��
��
�ʴ�Ϊ��3![]() ��
��