ЬтФПФкШн
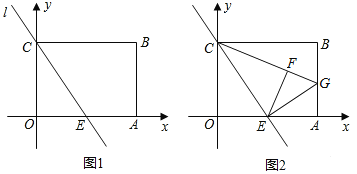
ЁОЬтФПЁПШчЭМЃЌжБЯпyЃНЉ![]() x+4гызјБъжсЗжБ№НЛгкЕуAЁЂBЃЌгыжБЯпyЃНxНЛгкЕуCЃЎдкЯпЖЮOAЩЯЃЌЖЏЕуQвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШДгЕуOГіЗЂЯђЕуAзідШЫйдЫЖЏЃЌЭЌЪБЖЏЕуPДгЕуAГіЗЂЯђЕуOзідШЫйдЫЖЏЃЌЕБЕуPЁЂQЦфжавЛЕуЭЃжЙдЫЖЏЪБЃЌСэвЛЕувВЭЃжЙдЫЖЏЃЎЗжБ№Й§ЕуPЁЂQзїxжсЕФДЙЯпЃЌНЛжБЯпABЁЂOCгкЕуEЁЂFЃЌСЌНгEFЃЎШєдЫЖЏЪБМфЮЊtУыЃЌдкдЫЖЏЙ§ГЬжаЫФБпаЮPEFQзмЮЊОиаЮЃЈЕуPЁЂQжиКЯГ§ЭтЃЉЃЎ
x+4гызјБъжсЗжБ№НЛгкЕуAЁЂBЃЌгыжБЯпyЃНxНЛгкЕуCЃЎдкЯпЖЮOAЩЯЃЌЖЏЕуQвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШДгЕуOГіЗЂЯђЕуAзідШЫйдЫЖЏЃЌЭЌЪБЖЏЕуPДгЕуAГіЗЂЯђЕуOзідШЫйдЫЖЏЃЌЕБЕуPЁЂQЦфжавЛЕуЭЃжЙдЫЖЏЪБЃЌСэвЛЕувВЭЃжЙдЫЖЏЃЎЗжБ№Й§ЕуPЁЂQзїxжсЕФДЙЯпЃЌНЛжБЯпABЁЂOCгкЕуEЁЂFЃЌСЌНгEFЃЎШєдЫЖЏЪБМфЮЊtУыЃЌдкдЫЖЏЙ§ГЬжаЫФБпаЮPEFQзмЮЊОиаЮЃЈЕуPЁЂQжиКЯГ§ЭтЃЉЃЎ
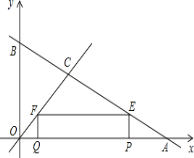
ЃЈ1ЃЉЧѓЕуPдЫЖЏЕФЫйЖШЪЧЖрЩйЃП
ЃЈ2ЃЉЕБtЮЊЖрЩйУыЪБЃЌОиаЮPEFQЮЊе§ЗНаЮЃП
ЁОД№АИЁПЃЈ1ЃЉЕуPдЫЖЏЕФЫйЖШЪЧУПУы2ИіЕЅЮЛГЄЖШЃЛЃЈ2ЃЉtЃН2Лђ4ЃЛ
ЁОНтЮіЁП
ЃЈ1ЃЉЯШЧѓЕУAЃЌBСНЕузјБъЃЌЕУЕН![]() ЕФжЕЃЌдйИљОнЯрЫЦШ§НЧаЮЖдгІБпГЩБШР§ЕУЕНAPгыEPЕФБШжЕЃЌНјЖјЕУЕНЕуPЕФЫйЖШЃЛ
ЕФжЕЃЌдйИљОнЯрЫЦШ§НЧаЮЖдгІБпГЩБШР§ЕУЕНAPгыEPЕФБШжЕЃЌНјЖјЕУЕНЕуPЕФЫйЖШЃЛ
ЃЈ2ЃЉЗжQЃЌPСНЕуЯргіЧАКѓСНжжЧщПіНјааЬжТлЃЌЕБPQЃНPEЪБЃЌОиаЮPEFQЮЊе§ЗНаЮЃЌгЩгУЙигкtЕФЪНзгБэЪОИїЯпЖЮЕФГЄЃЌШЛКѓЧѓГіtЕФжЕМДПЩ.
НтЃКЃЈ1ЃЉЁпжБЯпyЃНЉ![]() x+4гызјБъжсЗжБ№НЛгкЕуAЁЂBЃЌ
x+4гызјБъжсЗжБ№НЛгкЕуAЁЂBЃЌ
ЁрxЃН0ЪБЃЌyЃН4ЃЌyЃН0ЪБЃЌxЃН8ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЕБtУыЪБЃЌQOЃНFQЃНtЃЌдђEPЃНtЃЌ
ЁпEPЁЮBOЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрAPЃН2tЃЌ
ЁпЖЏЕуQвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШДгЕуOГіЗЂЯђЕуAзідШЫйдЫЖЏЃЌ
ЁрЕуPдЫЖЏЕФЫйЖШЪЧУПУы2ИіЕЅЮЛГЄЖШЃЛ
ЃЈ2ЃЉШчЭМЃЌЕБPQЃНPEЪБЃЌОиаЮPEFQЮЊе§ЗНаЮЃЌ
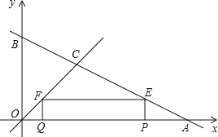
дђЁпOQЃНFQЃНtЃЌPAЃН2tЃЌ
ЁрQPЃН8ЉtЉ2tЃН8Љ3tЃЌ
Ёр8Љ3tЃНtЃЌ
НтЕУЃКtЃН2ЃЛ
ШчЭМ2ЃЌЕБPQЃНPEЪБЃЌОиаЮPEFQЮЊе§ЗНаЮЃЌ
ЁпOQЃНtЃЌPAЃН2tЃЌ
ЁрOPЃН8Љ2tЃЌ
ЁрQPЃНtЉЃЈ8Љ2tЃЉЃН3tЉ8ЃЌ
ЁрtЃН3tЉ8ЃЌ
НтЕУЃКtЃН4ЃЛ
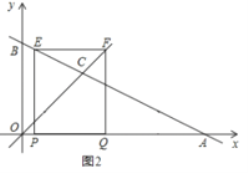

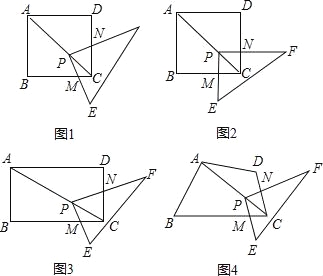
ЁОЬтФПЁПШчЭМЃЌжБЯп![]() КЭ
КЭ![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌ
ЃЌ![]() ЃЌдкЩфЯп
ЃЌдкЩфЯп![]() ЩЯШЁвЛЕу
ЩЯШЁвЛЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЩЯЕФвЛИіЖЏЕу(ВЛгыЕу
ЩЯЕФвЛИіЖЏЕу(ВЛгыЕу![]() жиКЯ)ЃЌЙ§Еу
жиКЯ)ЃЌЙ§Еу![]() зї
зї![]() ЕФДЙЯпНЛЩфЯп
ЕФДЙЯпНЛЩфЯп![]() гкЕу
гкЕу![]() .
.
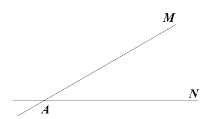
(1)ШЗЖЈЕу![]() ЕФЮЛжУЃЌдкЯпЖЮ
ЕФЮЛжУЃЌдкЯпЖЮ![]() ЩЯШЮШЁвЛЕу
ЩЯШЮШЁвЛЕу![]() ЃЌИљОнЬтвтЃЌВЙШЋЭМаЮЃЛ
ЃЌИљОнЬтвтЃЌВЙШЋЭМаЮЃЛ
(2)Щш![]() cmЃЌ
cmЃЌ![]() cmЃЌЬНОПКЏЪ§
cmЃЌЬНОПКЏЪ§![]() ЫцздБфСП
ЫцздБфСП![]() ЕФБфЛЏЖјБфЛЏЕФЙцТЩ.
ЕФБфЛЏЖјБфЛЏЕФЙцТЩ.
ЂйЭЈЙ§ШЁЕуЁЂЛЭМЁЂВтСПЃЌЕУЕНСЫ![]() гы
гы![]() ЕФМИзщЖдгІжЕЃЌШчЯТБэЃК
ЕФМИзщЖдгІжЕЃЌШчЯТБэЃК
|
|
|
|
|
|
|
|
|
|
|
|
|
(вЊЧѓЃКВЙШЋБэИёЃЌЯрЙиЪ§жЕБЃСєвЛЮЛаЁЪ§)
Ђк)НЈСЂЦНУцжБНЧзјБъЯЕ![]() ЃЌУшГівдВЙШЋКѓЕФБэжаИїЖдгІжЕЮЊзјБъЕФЕуЃЌЛГіИУКЏЪ§ЕФЭМЯѓЃЛ
ЃЌУшГівдВЙШЋКѓЕФБэжаИїЖдгІжЕЮЊзјБъЕФЕуЃЌЛГіИУКЏЪ§ЕФЭМЯѓЃЛ

ЂлНсКЯЛГіЕФКЏЪ§ЭМЯѓЃЌНтОіЮЪЬтЃКЕБ![]() ЮЊ
ЮЊ![]() аББп
аББп![]() ЩЯЕФжаЯпЪБЃЌ
ЩЯЕФжаЯпЪБЃЌ![]() ЕФГЄЖШдМЮЊ_____cm(НсЙћБЃСєвЛЮЛаЁЪ§).
ЕФГЄЖШдМЮЊ_____cm(НсЙћБЃСєвЛЮЛаЁЪ§).