题目内容
“文昌阁”是扬州的标志.某天,小芳、小丽来到文昌阁,准备用她们所学的知识测算它的高度.如图,小芳站在A处测得她看塔顶的仰角α为45°,小丽站在B处(A、B与塔的轴心共线)测得她看塔顶的仰角β为30°.她们又测出A、B两点的距离为15米.已知她们的目高(眼睛到地面的距离)均为1.5m,则可计算出塔高约为多少米?(结果精确到1m,参考数据:
≈1.4,
≈1.7)

| 2 |
| 3 |

考点:解直角三角形的应用-仰角俯角问题
专题:
分析:首先过点C作CE⊥AB于E,交DE于F,根据题意可得:AE⊥AB,BD⊥AB,DE∥AB,即可证得四边形ABDE是矩形,EF=AE=BD=1.5m,CF⊥DE,然后设CF=xm,分别在Rt△CEF中与Rt△CDF中,利用正切函数,即可表示出EF与DF的长,继而可得方程:
x-x=15,解此方程即可求得答案.
| 3 |
解答: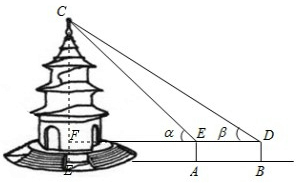 解:过点C作CE⊥AB于E,交DE于F,
解:过点C作CE⊥AB于E,交DE于F,
根据题意得:AE⊥AB,BD⊥AB,DE∥AB,
∴四边形ABDE是矩形,EF=AE=BD=1.5m,CF⊥DE,
∴DE=AB=15m,
设CF=xm,
在Rt△CEF中,EF=
=
=x(m),
在Rt△CDF中,DF=
=
=
x(m),
∴
x-x=15,
解得:x=
≈20.25(m),
∴CE=CF+EF=20.25+1.5=21.75(m).
答:塔高约为21.75m.
 解:过点C作CE⊥AB于E,交DE于F,
解:过点C作CE⊥AB于E,交DE于F,根据题意得:AE⊥AB,BD⊥AB,DE∥AB,
∴四边形ABDE是矩形,EF=AE=BD=1.5m,CF⊥DE,
∴DE=AB=15m,
设CF=xm,
在Rt△CEF中,EF=
| CF |
| tanα |
| x |
| tan45° |
在Rt△CDF中,DF=
| CF |
| tanβ |
| x |
| tan30° |
| 3 |
∴
| 3 |
解得:x=
15(
| ||
| 2 |
∴CE=CF+EF=20.25+1.5=21.75(m).
答:塔高约为21.75m.
点评:本题考查仰角的定义.此题难度适中,注意要能借助仰角构造直角三角形并解直角三角形是解此题的关键,注意数形结合与方程思想的应用.

练习册系列答案
相关题目
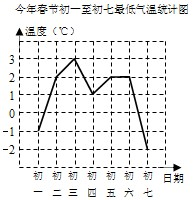 小华同学根据某地今年春节初一至初七的每天最低气温绘成了所示的折线统计图.关于这7天的每天最低气温的说法不正确的是( )
小华同学根据某地今年春节初一至初七的每天最低气温绘成了所示的折线统计图.关于这7天的每天最低气温的说法不正确的是( )| A、极差是5℃ |
| B、众数是2℃ |
| C、中位数是1℃ |
| D、平均数是1℃ |
已知存在实数A、B、C使得等式
=
-
总成立,则A+B+C=( )
| A |
| x-1 |
| x+1 |
| x3- 2x+1 |
| Bx+C |
| x2+x-1 |
| A、-3 | B、3 | C、2 | D、0 |
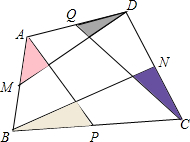 如图,在四边形ABCD中,M为AB的中点,P为BC的中点,N为CD的中点,Q为DA的中点,若图中中间的小四边形的面积为1,试求四个小三角形(阴影部分)面积之和.
如图,在四边形ABCD中,M为AB的中点,P为BC的中点,N为CD的中点,Q为DA的中点,若图中中间的小四边形的面积为1,试求四个小三角形(阴影部分)面积之和.
 已知△ABC中,AD与BE交于点F,且AE:EC=3:2,BD:BC=1:3,求S△ABF:S四边形DCEF.
已知△ABC中,AD与BE交于点F,且AE:EC=3:2,BD:BC=1:3,求S△ABF:S四边形DCEF.