题目内容
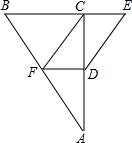 已知:如图在△ABC中,∠ACB=90°,D是AC的中点,DF∥BC,点E在BC的延长线上,且DE=AF.求证:
已知:如图在△ABC中,∠ACB=90°,D是AC的中点,DF∥BC,点E在BC的延长线上,且DE=AF.求证:(1)△ADF≌△DCE;
(2)△ADF≌△CDF.
考点:全等三角形的判定
专题:证明题
分析:(1)D是AC的中点可得AD=CD,DF∥BC且∠ACB=90°可得∠ADF=∠DCE=90°,且DE=AF,所以可证得△ADF≌△DCE;
(2)AD=CD,∠ADF=∠CDF=90°,且DF为公共边,所以可证得△ADF≌△CDF.
(2)AD=CD,∠ADF=∠CDF=90°,且DF为公共边,所以可证得△ADF≌△CDF.
解答:证明:
(1)∵D是AC的中点,
∴AD=CD,
∵DF∥BC且∠ACB=90°,
∴∠ADF=∠DCE=90°,
在Rt△ADF和Rt△DCE中
∴△ADF≌△DCE;
(2)∵D是AC的中点,
∴AD=CD,
∵DF∥BC且∠ACB=90°,
∴∠ADF=∠DCF=90°,
在Rt△ADF和Rt△DCE中
∴△ADF≌△CDF.
(1)∵D是AC的中点,
∴AD=CD,
∵DF∥BC且∠ACB=90°,
∴∠ADF=∠DCE=90°,
在Rt△ADF和Rt△DCE中
|
∴△ADF≌△DCE;
(2)∵D是AC的中点,
∴AD=CD,
∵DF∥BC且∠ACB=90°,
∴∠ADF=∠DCF=90°,
在Rt△ADF和Rt△DCE中
|
∴△ADF≌△CDF.
点评:本题主要考查三角形全等的判定,解题的关键是掌握好常用的几种方法,即:SSS,SAS,ASA,AAS,HL.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
将分式
中分子与分母的各项系数都化成整数,正确的是( )
| ||
| a+0.5b |
A、
| ||
B、
| ||
C、
| ||
D、
|
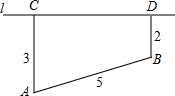 已知,河岸l同侧有A、B两镇,A、B到L的距离CA=3,BD=2,AB=5,在l上找一点P,使PA=PB.
已知,河岸l同侧有A、B两镇,A、B到L的距离CA=3,BD=2,AB=5,在l上找一点P,使PA=PB.