题目内容
 如图,一次函数y=-2x+t(t>0)的图象与x轴,y轴分别交于点C,D.
如图,一次函数y=-2x+t(t>0)的图象与x轴,y轴分别交于点C,D.(1)求点C,点D的坐标;
(2)已知点P是二次函数y=-x2+3x图象在y轴右侧部分上的一个动点,若以点C,点D为直角顶点的△PCD与△OCD相似.求t的值及对应的点P的坐标.
分析:(1)令一次函数解析式中y=0,求出对应x的值,确定出C的坐标,令x=0,求出对应y的值,确定出D的坐标即可;
(2)由(1)得出的C与D的坐标,求出OC及OD的长,在直角三角形OCD中,利用勾股定理表示出CD,以CD为直角边的△PCD与△OCD相似,过P作PM⊥y轴,PN⊥x轴,如图中红线所示,以D为直角顶点的△PCD与△OCD相似,此时∠CDP=90°,分两种情况考虑:当PD:DC=OC:OD=1:2时,由表示出的DC得到PD的长,根据P在二次函数图象上,设P的坐标为(x,-x2+3x),表示出PM与MD,在直角三角形PMD中,利用勾股定理列出关系式,记作①,表示出CN,在直角三角形PCD与直角三角形PCN中,分别利用勾股定理表示出PC2,将各自的值代入得到关系式,记作②,联立①②可得出t与x的值,进而确定出此时P的坐标;若DC:PD=OC:OD=1:2时,如图所示,同理可以求得t与x的值,确定出此时P的坐标,综上,得到所有满足题意t的值及对应P的坐标.
(2)由(1)得出的C与D的坐标,求出OC及OD的长,在直角三角形OCD中,利用勾股定理表示出CD,以CD为直角边的△PCD与△OCD相似,过P作PM⊥y轴,PN⊥x轴,如图中红线所示,以D为直角顶点的△PCD与△OCD相似,此时∠CDP=90°,分两种情况考虑:当PD:DC=OC:OD=1:2时,由表示出的DC得到PD的长,根据P在二次函数图象上,设P的坐标为(x,-x2+3x),表示出PM与MD,在直角三角形PMD中,利用勾股定理列出关系式,记作①,表示出CN,在直角三角形PCD与直角三角形PCN中,分别利用勾股定理表示出PC2,将各自的值代入得到关系式,记作②,联立①②可得出t与x的值,进而确定出此时P的坐标;若DC:PD=OC:OD=1:2时,如图所示,同理可以求得t与x的值,确定出此时P的坐标,综上,得到所有满足题意t的值及对应P的坐标.
解答:解:(1)对于一次函数y=-2x+t,
令y=0,求出x=
,令x=0,求出y=t,
∴C坐标为(
,0),D坐标为(0,t);
(2)由(1)得:OD=t,OC=
,
在Rt△OCD中,根据勾股定理得:CD=
=
,
以D为直角顶点的△PCD与△OCD相似,此时∠CDP=90°,
过P作PM⊥y轴,PN⊥x轴,如图中红线所示:
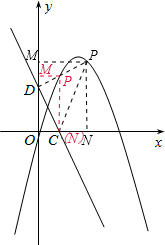
若PD:DC=OC:OD=1:2,则PD=
,
设P(x,-x2+3x),
∴PM=ON=x,PN=OM=-x2+3x,MD=-x2+3x-t,
在Rt△PMD中,根据勾股定理得:PD2=PM2+MD2,
∴(
)2=x2+(-x2+3x-t)2,①
又CN=ON-OC=x-
,
∴在Rt△PDC与Rt△PCN中,利用勾股定理得:PC2=PD2+CD2=PN2+CN2,
∴(
)2+(
)2=(-x2+3x)2+(x-
)2,②
联立①②解得:x=
,t=1,
∴此时P坐标为(
,
);
若DC:PD=OC:OD=1:2时,如图所示,同理可以求得t=1,P(2,2),
若以C为直角顶点时,△PCD与△OCD相似,此时∠DCP=90°时,同理可得t=
,P(
,
),
综上,当t=1时,对应的P坐标为(
,
)或(2,2)或P(
,
)
令y=0,求出x=
| t |
| 2 |
∴C坐标为(
| t |
| 2 |
(2)由(1)得:OD=t,OC=
| t |
| 2 |
在Rt△OCD中,根据勾股定理得:CD=
| OD2+OC2 |
| ||
| 2 |
以D为直角顶点的△PCD与△OCD相似,此时∠CDP=90°,
过P作PM⊥y轴,PN⊥x轴,如图中红线所示:

若PD:DC=OC:OD=1:2,则PD=
| ||
| 4 |
设P(x,-x2+3x),
∴PM=ON=x,PN=OM=-x2+3x,MD=-x2+3x-t,
在Rt△PMD中,根据勾股定理得:PD2=PM2+MD2,
∴(
| ||
| 4 |
又CN=ON-OC=x-
| t |
| 2 |
∴在Rt△PDC与Rt△PCN中,利用勾股定理得:PC2=PD2+CD2=PN2+CN2,
∴(
| ||
| 4 |
| ||
| 2 |
| t |
| 2 |
联立①②解得:x=
| 1 |
| 2 |
∴此时P坐标为(
| 1 |
| 2 |
| 5 |
| 4 |
若DC:PD=OC:OD=1:2时,如图所示,同理可以求得t=1,P(2,2),
若以C为直角顶点时,△PCD与△OCD相似,此时∠DCP=90°时,同理可得t=
| 26 |
| 25 |
| 13 |
| 5 |
| 26 |
| 25 |
综上,当t=1时,对应的P坐标为(
| 1 |
| 2 |
| 5 |
| 4 |
| 13 |
| 5 |
| 26 |
| 25 |
点评:此题考查了二次函数的性质,一次函数与坐标轴的交点,勾股定理,相似三角形的判定与性质,以及坐标与图形性质,利用了数形结合及分类讨论的思想,是一道综合性较强的压轴题.

练习册系列答案
相关题目
 已知,如图,一次函数y1=-x-1与反比例函数y2=-
已知,如图,一次函数y1=-x-1与反比例函数y2=-| 2 |
| x |
| A、x>1 |
| B、x<-2或0<x<1 |
| C、-2<x<1 |
| D、-2<x<0或x>1 |
 如图,一次函数y=kx+2的图象与反比例函数y=
如图,一次函数y=kx+2的图象与反比例函数y= 13、如图,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是
13、如图,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是 (2013•成都)如图,一次函数y1=x+1的图象与反比例函数
(2013•成都)如图,一次函数y1=x+1的图象与反比例函数 如图,一次函数y=x+3的图象与x轴、y轴分别交于点A、点B,与反比例函数
如图,一次函数y=x+3的图象与x轴、y轴分别交于点A、点B,与反比例函数