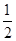题目内容
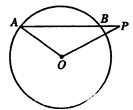
已知:如图,在矩形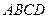 中,点
中,点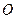 在对角线
在对角线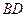 上,以
上,以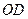 的长为半径的⊙
的长为半径的⊙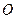 与
与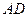 ,
,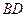 分别交于点E、点F,且∠
分别交于点E、点F,且∠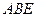 =∠
=∠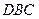 .
.
(1)判断直线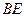 与⊙
与⊙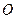 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;
(2)若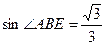 ,
,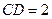 ,求⊙
,求⊙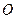 的半径.
的半径.
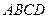 中,点
中,点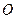 在对角线
在对角线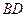 上,以
上,以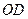 的长为半径的⊙
的长为半径的⊙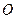 与
与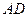 ,
,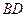 分别交于点E、点F,且∠
分别交于点E、点F,且∠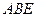 =∠
=∠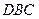 .
.(1)判断直线
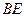 与⊙
与⊙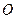 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;
(2)若
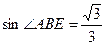 ,
,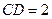 ,求⊙
,求⊙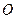 的半径.
的半径.解:(1)直线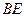 与⊙O相切……………………………………………………1分
与⊙O相切……………………………………………………1分
证明:联结
在矩形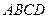 中,
中, 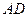 ∥
∥
∴∠ =∠
=∠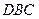
∵
∴∠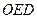 =∠
=∠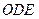
又∵∠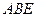 =∠
=∠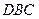
∴∠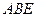 =∠
=∠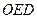 ……………………………………………………………2分
……………………………………………………………2分
∵矩形 ,∠
,∠
∴
∴
∴ ………………………………………………………………3分
………………………………………………………………3分
∴直线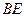 与⊙O相切
与⊙O相切
(2) 联结
方法1:
∵四边形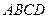 是矩形,
是矩形,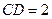
∴ ,
,
∵∠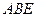 =∠
=∠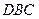
∴
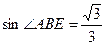
∴ …………………………………………………4分
…………………………………………………4分
在 中,可求
中,可求
∴勾股定理求得
在 中,
中,

设⊙O的半径为
则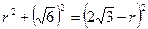
∴ =
= ………………………
……………………… ……………………………………………5分
……………………………………………5分
方法2:∵ 是⊙O的直径
是⊙O的直径
∴
∵四边形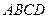 是矩形
是矩形
∴ ,
,
∵∠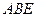 =∠
=∠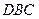
∴

设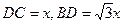 ,则
,则
∵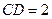
∴ ……………………………………………………………4分
……………………………………………………………4分
∵
∴
∴
∴
∴ 为
为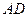 中点.
中点.
∵ 为直径,∠
为直径,∠
∴
∴
∴⊙O的半径为 ……………………………………………………………5分
……………………………………………………………5分
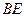 与⊙O相切……………………………………………………1分
与⊙O相切……………………………………………………1分证明:联结

在矩形
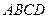 中,
中, 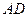 ∥
∥
∴∠
 =∠
=∠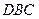
∵

∴∠
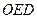 =∠
=∠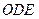
又∵∠
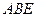 =∠
=∠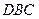
∴∠
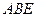 =∠
=∠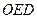 ……………………………………………………………2分
……………………………………………………………2分∵矩形
 ,∠
,∠
∴

∴

∴
 ………………………………………………………………3分
………………………………………………………………3分∴直线
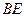 与⊙O相切
与⊙O相切(2) 联结

方法1:
∵四边形
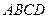 是矩形,
是矩形,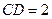
∴
 ,
,
∵∠
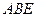 =∠
=∠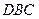
∴

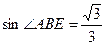
∴
 …………………………………………………4分
…………………………………………………4分在
 中,可求
中,可求
∴勾股定理求得

在
 中,
中,

设⊙O的半径为

则
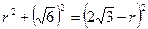
∴
 =
= ………………………
……………………… ……………………………………………5分
……………………………………………5分方法2:∵
 是⊙O的直径
是⊙O的直径∴

∵四边形
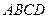 是矩形
是矩形∴
 ,
,
∵∠
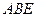 =∠
=∠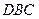
∴


设
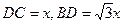 ,则
,则
∵
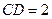
∴
 ……………………………………………………………4分
……………………………………………………………4分∵

∴

∴

∴

∴
 为
为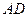 中点.
中点.∵
 为直径,∠
为直径,∠
∴

∴

∴⊙O的半径为
 ……………………………………………………………5分
……………………………………………………………5分略

练习册系列答案
相关题目
 (2)
(2)

 或
或
 的边OA上一点,且P点的坐标为(3,4),则sin
的边OA上一点,且P点的坐标为(3,4),则sin

 ≈1.73,计算结果保留整数)
≈1.73,计算结果保留整数)