题目内容
(本题满分8分)已知一元二次方程 .
.
(1)若方程有两个实数根,求m的范围;
(2)若方程的两个实数根为 ,
, ,且
,且 +3
+3 =3,求m的值.
=3,求m的值.
(1)m≤1;(2)m= .
.
【解析】
试题分析:(1)根据一元二次方程的根的判别式可知,当方程有两个实数根时,则△≥0;
(2)根据根与系数的关系可知 ,又有
,又有 ,联立方程组解得方程的解,应用方程的解的定义,把一个根代入方程,求得字母系数m的值.
,联立方程组解得方程的解,应用方程的解的定义,把一个根代入方程,求得字母系数m的值.
试题解析:(1)因为一元二次方程 -2x+m=0有两个实数根,则△=
-2x+m=0有两个实数根,则△= -4ac=
-4ac= -4×1×m≥0,则4-4m≥0,解得m≤1;
-4×1×m≥0,则4-4m≥0,解得m≤1;
(2)根据根与系数的关系可得: ①,而
①,而 ②,
②,
把②-①得: ,
, ,
,
代入原方程得: , 解得:m=
, 解得:m= .
.
考点:一元二次方程的根的判别式;根与系数的关系.
考点分析: 考点1:一元二次方程 定义:只含有一个未知数,并且未知数的最高次数是2的整式方程叫做一元二次方程。
一元二次方程的一般形式:

它的特征是:等式左边是一个关于未知数x的二次多项式,等式右边是零,其中 ax2叫做二次项,a叫做二次项系数;bx叫做一次项,b叫做一次项系数;c叫做常数项。 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
 -3kxy-3
-3kxy-3 +6xy-8不含xy项,则k= ;
+6xy-8不含xy项,则k= ; ≈1.7)
≈1.7)
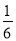 B.
B.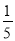 C.
C.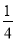 D.
D.
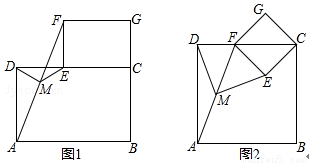
 中,
中, 、
、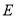 分别是边
分别是边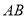 、
、 的中点,
的中点, .现将
.现将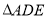 沿
沿 折叠,点
折叠,点 落在三角形所在平面内的点为
落在三角形所在平面内的点为 ,则
,则 的度数为 °.
的度数为 °.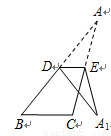
 有意义,则
有意义,则 的取值范围是 .
的取值范围是 .
 ),
),