题目内容
如图,在△ABC中,AB=AC=2,∠A=90°,点P为BC的中点,点E、F分别为边AB、AC上的点,若∠EPF=45°,若∠FEP=60°,则CF= .

 .
.
【解析】
试题分析:过点F作FM⊥PE,垂足为M,设EM=a,由特殊角的三角函数值可得FM=DM= ,PE=a+
,PE=a+ ,PF=
,PF= ,在Rt△ABC中,BC=
,在Rt△ABC中,BC= ,所以BP=CP=
,所以BP=CP= ,因为∠EPF=45°,∠C=45°,所以∠1+∠2=∠2+∠3,所以∠1=∠3,又∠B=∠C=45°,所以△BPE∽△CFP,所以
,因为∠EPF=45°,∠C=45°,所以∠1+∠2=∠2+∠3,所以∠1=∠3,又∠B=∠C=45°,所以△BPE∽△CFP,所以 ,即
,即 ,解得:CF=
,解得:CF= .
.

考点:特殊角的三角函数值;相似三角形的判定和性质.
考点分析: 考点1:三角形 (1)三角形的概念:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.组成三角形的线段叫做三角形的边.
相邻两边的公共端点叫做三角形的顶点.
相邻两边组成的角叫做三角形的内角,简称三角形的角.
(2)按边的相等关系分类:不等边三角形和等腰三角形(底和腰不等的等腰三角形、底和腰相等的等腰三角形即等边三角形).
(3)三角形的主要线段:角平分线、中线、高.
(4)三角形具有稳定性. 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目

 C.
C. D.
D.
 .
. ,
, ,且
,且 +3
+3 =3,求m的值.
=3,求m的值.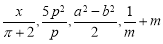 ,其中分式共有( ).
,其中分式共有( ). 经过
经过 上的点
上的点 ,并且
,并且 ,
, ,
, 交直线
交直线 于
于 ,连接
,连接 .
. [
[ 是
是 的切线;
的切线; ,
, 的半径为3,求
的半径为3,求 的长.
的长. = ;
= ;