题目内容
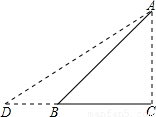
(2003•盐城)如图所示,在平行四边形ABCD中,AC与BD相交于点O,AB⊥AC,∠DAC=45°,AC=2,求BD的长.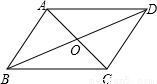
【答案】分析:根据已知条件得到等腰直角三角形ABC,则AB=AC=2,又根据平行四边形的对角线互相平分,得到OA=1,根据勾股定理就可求得OB的长,再根据平行四边形的对角线互相平分,就可求得BD的长.
解答:解:∵四边形ABCD是平行四边形,∠DAC=45°,
∴∠ACB=∠DAC=45°,OA= AC=1,
AC=1,
∵AB⊥AC,
∴△ABC是等腰直角三角形,
∴AB=AC=2,
在Rt△AOB中,根据勾股定理得OB= ,
,
∴BD=2BO=2 .
.
点评:此题要求学生熟练运用等腰直角三角形的性质和勾股定理;熟悉平行四边形的性质.
解答:解:∵四边形ABCD是平行四边形,∠DAC=45°,
∴∠ACB=∠DAC=45°,OA=
 AC=1,
AC=1,∵AB⊥AC,
∴△ABC是等腰直角三角形,
∴AB=AC=2,
在Rt△AOB中,根据勾股定理得OB=
 ,
,∴BD=2BO=2
 .
.点评:此题要求学生熟练运用等腰直角三角形的性质和勾股定理;熟悉平行四边形的性质.

练习册系列答案
相关题目
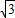 ,求抛物线的解析式;
,求抛物线的解析式;
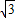 ,求抛物线的解析式;
,求抛物线的解析式;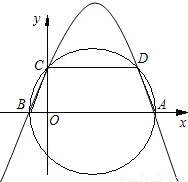
 (2003•盐城)如图,已知在△ABC中,∠ACB=90°,∠B=35°,为C为圆心、CA为半径的圆交AB于D点,则弧AD为 度.
(2003•盐城)如图,已知在△ABC中,∠ACB=90°,∠B=35°,为C为圆心、CA为半径的圆交AB于D点,则弧AD为 度.