题目内容
已知△ABC内接于⊙O,D是BC或其延长线上一点,AE是△ABC外接圆的一条弦,若∠BAE=∠CAD.求证:AD•AE为定值.
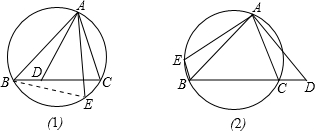
证明:如图(1),当点D是BC上任意一点且∠BAE=∠CAD时,连接BE,
则∠E=∠C,
∠BAE=∠CAD,
∴△ABE∽△ADC.
∴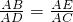 ,
,
即AD•AE=AB•AC为定值.
如图(2),当点D在BC的延长线上时,
∠BAE=∠CAD.此时,∠ACD=∠AEB.
∴△AEB∽△ACD,
∴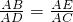
即AD•AE=AB•AC为定值.
综上所述,当点D在BC边上或其延长线上时,
只要∠CAD=∠BAE,总有AD•AE为定值.
分析:由于题干中D是BC或其延长线上一点,所以应分两种情况进行讨论;
(1)连BE,可得△ABE∽△ADC,进而可得结论;
(2)当其在BC的延长线上时,同样亦可得△AEB∽△ACD,所以当点D在BC边上或其延长线上时,总有AD•AE为定值.
点评:本题主要考查了相似三角形的判定及性质问题,可先探求定值,当AD⊥BC,AE为圆的直径时,满足∠BAE=∠CAD这一条件,不难发现△ACD∽△AEB,所以AD•AE=AB•AC,因为已知AB,AC均为定值.再就一般情况分点D在BC上,点D在BC的延长线上两种情况分别证明.
则∠E=∠C,
∠BAE=∠CAD,
∴△ABE∽△ADC.
∴
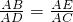 ,
,即AD•AE=AB•AC为定值.
如图(2),当点D在BC的延长线上时,
∠BAE=∠CAD.此时,∠ACD=∠AEB.
∴△AEB∽△ACD,
∴
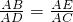
即AD•AE=AB•AC为定值.
综上所述,当点D在BC边上或其延长线上时,
只要∠CAD=∠BAE,总有AD•AE为定值.
分析:由于题干中D是BC或其延长线上一点,所以应分两种情况进行讨论;
(1)连BE,可得△ABE∽△ADC,进而可得结论;
(2)当其在BC的延长线上时,同样亦可得△AEB∽△ACD,所以当点D在BC边上或其延长线上时,总有AD•AE为定值.
点评:本题主要考查了相似三角形的判定及性质问题,可先探求定值,当AD⊥BC,AE为圆的直径时,满足∠BAE=∠CAD这一条件,不难发现△ACD∽△AEB,所以AD•AE=AB•AC,因为已知AB,AC均为定值.再就一般情况分点D在BC上,点D在BC的延长线上两种情况分别证明.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
 如图,已知△ABC内接于⊙O,D是⊙O上一点,连接BD、CD、AC、BD交于点E.
如图,已知△ABC内接于⊙O,D是⊙O上一点,连接BD、CD、AC、BD交于点E.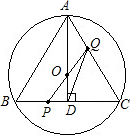 终点C运动,速度为1cm/s;点Q沿CA向终点A运动,速度为2cm/s,设它们运动的时间为x(s).
终点C运动,速度为1cm/s;点Q沿CA向终点A运动,速度为2cm/s,设它们运动的时间为x(s).
 (2013•樊城区模拟)如图,已知△ABC内接于⊙O,弦AD交BC于E,过点D的切线MN交直线AB于M,交直线AC于N.
(2013•樊城区模拟)如图,已知△ABC内接于⊙O,弦AD交BC于E,过点D的切线MN交直线AB于M,交直线AC于N. (2013•永州)如图,已知△ABC内接于⊙O,BC是⊙O的直径,MN与⊙O相切,切点为A,若∠MAB=30°,则∠B=
(2013•永州)如图,已知△ABC内接于⊙O,BC是⊙O的直径,MN与⊙O相切,切点为A,若∠MAB=30°,则∠B=