Question

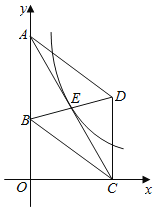
【题目】如图，在平面直角坐标系中，平行四边形ABCD的边AB在y轴上，点D（4，4），cos∠BCD＝，若反比例函数y＝（k≠0）的图象经过平行四边形对角线的交点E，则k的值为（ ）

A.14B.7C.8D.

Answer 1

【答案】B

【解析】

过点B作BG⊥CD于点G，根据D（4，4）和勾股定理可得，CG＝OB＝3，OA＝OB+AB＝7，过点E作EF⊥x轴于点F，可得EF∥AO，所以EF是三角形AOC的中位线，进而可求EF和OF的长，即可得k的值．

解：如图，过点B作BG⊥CD于点G，

∵D（4，4），

∴DC＝OC＝BG＝4，

∵cos∠BCD＝＝，

∴设CG＝3x，则BC＝5x，BG＝4，

根据勾股定理，得x＝1，

∴CG＝OB＝3，

∵四边形ABCD是平行四边形，

∴AB＝CD＝4，

∴OA＝OB+AB＝7，

过点E作EF⊥x轴于点F，

∴EF∥AO，

∵平行四边形对角线的交点E，

∴AE＝CE，EF∥AO，

∴OF＝CF，

∴EF是三角形AOC的中位线，

∴EF＝OA＝，

OF＝OC＝2，

∴k＝EFOF＝7，

故选：B．