��Ŀ����
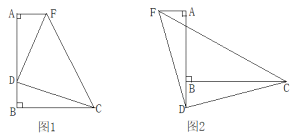
����Ŀ����ͼ��������ABCD�У�AB��a����ABC��60�㣬����A��AE��BC������ΪE��AF��CD������ΪF��
��1������EF���õ�ʽ��ʾ�߶�EF��EC��������ϵ����˵�����ɣ�
��2������BF������A��AK��BF������ΪK����BK�ij����ú�a�Ĵ���ʽ��ʾ����
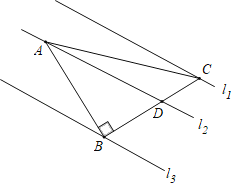
��3���ӳ��߶�CB��G���ӳ��߶�DC��H����BG��CH������AG��GH��AH��
���жϡ�AGH����״����˵�����ɣ�
����a��2��S��ADH��![]() ��3+
��3+![]() ������sin��GAB��ֵ��
������sin��GAB��ֵ��
���𰸡���1��EF��![]() EC�����ɼ���������2��BK��
EC�����ɼ���������2��BK��![]() ����3������AGHΪ�ȱ������Σ����ɼ���������sin��GAB��
����3������AGHΪ�ȱ������Σ����ɼ���������sin��GAB��![]() ��
��
��������
(1)�������ε����ʵó��߶κͽǶ����,�����Ƴ���AEB�ա�AFD,��ͨ������֤����AEFΪ�ȱ�������,���ݵȱ������ε��������EF����.
(2)�������Ǻ������BK����.
(3)�ٸ������⻭��ͼ��,����������ȫ��֤���������һ��Ϊ60�㼴��֤����AGHΪ�ȱ�������;�ڹ���C��CM��AH�ڵ�M,ͨ����ADH��������DH,�Ӷ����CH��HF,��֤����AFH�ǵ���ֱ��������,���������Ǻ����������.
������ABCD�У���ABC��60�㣬���ABC����ACDΪ�����߳�Ϊa�ĵȱ������Σ�
��1����ͼ1����AB��AD����ABE����ADF����ADF����AEB��90�㣬
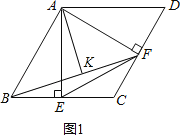
���AEB�ա�AFD��AAS����
��AE��AF��
�ڵȱߡ�ABC�У���AE��BC��
��AE�ǡ�BAC�Ľ�ƽ���ߣ��ʡ�BAE��30�㣬
ͬ����DAF��30�㣬
�ߡ�ABC��60�㣬���BAD��120�㣬
���EAF����BAD����BAE����DAF��120�㩁30�㩁30�㣽60�㣬
���AEFΪ�ȱ������Σ�
�ڵȱ�������ABC�У�AE��ABsin��ABC��![]() a��EF��AF��BE��EC��
a��EF��AF��BE��EC��![]() a��
a��
��EF��![]() EC��
EC��
��2����ͼ1����BAF����BAD����FAD��90�㣬
��Rt��ABF��tan��ABF��![]() ��
��![]() ��
��![]() ����cos��ABF��
����cos��ABF��![]() ��
��
��Rt��ABK��BK��ABcos��ABF��a��![]() ��
��![]() a��
a��
��3������ͼ2������AC��
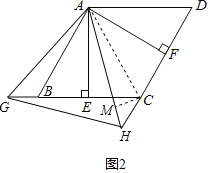
��BG��CH��AB��AC��
�֡ߡ�ABG��180�㩁��ABC��120�㣬��ACH��180�㩁ACD��120�㣽��ABG��
���ABG�ա�ACH��SAS����
��AG��AH����GAB����HAC��
���GAH����GAB+��BAH����HAC+��BAH����BAC��60�㣬
���AGHΪ�ȱ������Σ�
����ͼ2������C��CM��AH�ڵ�M��
S��ADH��![]() AF��DH��
AF��DH��![]() ��
��![]() ��2��DH��
��2��DH��![]() ��3+
��3+![]() ����
����
��ã�DH��![]() ��
��
CH��DH��CD��![]() ��
��
HF��DH��FD��![]() ��AF��
��AF��
���AFHΪ����ֱ�������Σ����AHC��45�㣬
��Rt��CHM��sin��MHC��![]() ��
��![]() ��sin45�㣽
��sin45�㣽![]() ��
��
��CM��![]() ��
��
��Rt��ACM��sin��HCM��![]() ��
��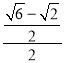 ��
��![]() ��sin��GAB��
��sin��GAB��
��sin��GAB��![]() ��
��