题目内容
 如图,CD是Rt△ABC斜边AB上的高,∠ACB=90°,AC=3,AD=2,则sinB的值是
如图,CD是Rt△ABC斜边AB上的高,∠ACB=90°,AC=3,AD=2,则sinB的值是
- A.

- B.

- C.

- D.

A
分析:将求sinB的值转化为求sin∠ACD的值,然后根据角的正弦值与三角形边的关系,求角的正弦值.
解答:由同角的余角相等得∠B=∠ACD.
∴sinB=sin∠ACD=AD:AC=2:3.
故选A.
点评:本题利用了锐角三角函数的概念和在直角三角形中,同角的余角相等而求解.
分析:将求sinB的值转化为求sin∠ACD的值,然后根据角的正弦值与三角形边的关系,求角的正弦值.
解答:由同角的余角相等得∠B=∠ACD.
∴sinB=sin∠ACD=AD:AC=2:3.
故选A.
点评:本题利用了锐角三角函数的概念和在直角三角形中,同角的余角相等而求解.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
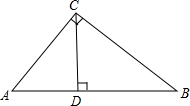 如图,CD是Rt△ABC斜边上的高.若AB=5,AC=3,则tan∠BCD为( )
如图,CD是Rt△ABC斜边上的高.若AB=5,AC=3,则tan∠BCD为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 5、如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于( )
5、如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于( ) 18、如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于
18、如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于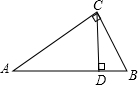 如图,CD是Rt△ABC斜边上的高线,若sinA=
如图,CD是Rt△ABC斜边上的高线,若sinA=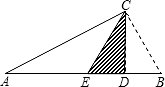 如图,CD是Rt△ABC斜边AB上的高,直角边AC=
如图,CD是Rt△ABC斜边AB上的高,直角边AC=