题目内容
9.计算(1)(π+1)0-$\sqrt{12}+|{-\sqrt{3}}$|
(2)${(\sqrt{5}-2)^2}+(\sqrt{5}+1)(\sqrt{5}+3)$
(3)$\frac{x^2}{x-y}-\frac{y^2}{x-y}$
(4)(1+$\frac{1}{x+1}$)÷$\frac{(x+2)(x-1)}{{{x^2}-1}}$.
分析 (1)根据零指数幂的意义得到原式=1-2$\sqrt{3}$+$\sqrt{3}$,然后合并即可;
(2)先利用乘法公式展开,然后合并即可;
(3)先进行同分母的减法运算,然后把分子分解后约分即可;
(4)先把括号内通分、除法运算化为乘法运算,然后约分即可.
解答 解:(1)原式=1-2$\sqrt{3}$+$\sqrt{3}$
=1-$\sqrt{3}$;
(2)原式=5-4$\sqrt{5}$+4+5+3$\sqrt{5}$+$\sqrt{5}$+3
=17;
(3)原式=$\frac{{x}^{2}-{y}^{2}}{x-y}$
=$\frac{(x+y)(x-y)}{x-y}$
=x+y;
(4)原式=$\frac{x+1+1}{x+1}$•$\frac{(x+1)(x-1)}{(x+2)(x-1)}$
=1.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了零指数幂和分式的混合运算.

练习册系列答案
相关题目
14.王老师自驾轿车沿高速公路从A地到B地旅游,途经两座跨海大桥,共用了4.5小时;返回时平均速度提高了10千米/小时,比去时少用了半小时回到A地.
(1)求A、B两地间的路程.
(2)两座跨海大桥的长度及过桥费见表.
该省交通部门规定:轿车的高速公路通行费y(元)的计算方法为:y=ax+b+5,其中a(元/千米)为高速公路里程费,x(千米)为高速公路里程(不包括跨海大桥长),b(元)为跨海大桥过桥费.若王老师从A地到B地所花的高速公路通行费为295.4元,求轿车的高速公路里程费a.
(1)求A、B两地间的路程.
(2)两座跨海大桥的长度及过桥费见表.
| 大桥名称 | 跨海大桥1 | 跨海大桥2 |
| 大桥长度 | 48千米 | 36千米 |
| 过桥费 | 100元 | 80元 |
 a,b,c三个数在数轴上的位置如图所示,化简:|a-b|-|a+c|-|c-b|.
a,b,c三个数在数轴上的位置如图所示,化简:|a-b|-|a+c|-|c-b|.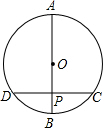 如图,⊙O的直径AB垂直弦CD于点P,且P是半径OB的中点,若CD=6cm,则⊙O的半径长为2$\sqrt{3}$cm.
如图,⊙O的直径AB垂直弦CD于点P,且P是半径OB的中点,若CD=6cm,则⊙O的半径长为2$\sqrt{3}$cm.