题目内容
如图,已知直径为OA的⊙P与x轴交于O、A两点,点B、C把 三等分,连接PC并延长PC交y轴于点D(0,3).
三等分,连接PC并延长PC交y轴于点D(0,3).
求证:(1)△POD≌△ABO;
(2)若直线l:y=kx+b经过圆心P和D,求直线l的解析式

【答案】
(1)证明见解析(2)y= x+3
x+3
【解析】(1)证明:连接PB,
∵直径为OA的⊙P与x轴交于O、A两点,点B、C把 三等分,
三等分,
∴∠APB=∠DPO= ×180°=60°,∠ABO=∠POD=90°。
×180°=60°,∠ABO=∠POD=90°。
∵PA=PB,∴△PAB是等边三角形。
∴AB=PA,∠BAO=60°,
∴AB=OP,∠BAO=∠OPD。
在△POD和△ABO中,
∵∠OPD=∠BAO, OP=BA ,∠POD=∠ABO ,
∴△POD≌△ABO(ASA)。
(2)解:由(1)得△POD≌△ABO,∴∠PDO=∠AOB。
∵∠AOB= ∠APB=
∠APB= ×60°=30°,∴∠PDO=30°。
×60°=30°,∴∠PDO=30°。
∴OP=OD•tan30°=3× 。∴点P的坐标为:(-
。∴点P的坐标为:(- ,0)。
,0)。
∵点P,D在直线y=kx+b上,
∴ ,解得:
,解得: 。
。
∴直线l的解析式为:y= x+3。
x+3。
(1)首先连接PB,由直径为OA的⊙P与x轴交于O、A两点,点B、C把 三等分,可求得∠APB=∠DPO=60°,∠ABO=∠POD=90°,即可得△PAB是等边三角形,可得AB=OP,然后由ASA,即可判定:△POD≌△ABO。
三等分,可求得∠APB=∠DPO=60°,∠ABO=∠POD=90°,即可得△PAB是等边三角形,可得AB=OP,然后由ASA,即可判定:△POD≌△ABO。
(2)易求得∠PDO=30°,由OP=OD•tan30°,即可求得点P的坐标,然后利用待定系数法,即可求得直线l的解析式。

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
相关题目
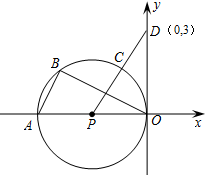 (2012•凉山州)如图,已知直径为OA的⊙P与x轴交于O、A两点,点B、C把
(2012•凉山州)如图,已知直径为OA的⊙P与x轴交于O、A两点,点B、C把
 P与x轴交于O、A两点,点B、C把
P与x轴交于O、A两点,点B、C把 三等分,连接PC并延长PC交y轴于点D(0,3).
三等分,连接PC并延长PC交y轴于点D(0,3). △ABO;
△ABO;
 三等分,连接PC并延长PC交y轴于点D(0,3).
三等分,连接PC并延长PC交y轴于点D(0,3).
 三等分,连接PC并延长PC交y轴于点D(0,3).
三等分,连接PC并延长PC交y轴于点D(0,3).