Question

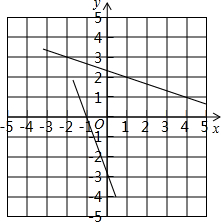如图，是在同一坐标系内作出的一次函数l₁、l₂的图象，设l₁：y=k₁x+b₁，l₂：y=k₂x+b₂，则方程组的解是________．

Answer 1

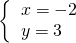
分析：由图得，函数y₁、y₂的图象l₁、l₂，分别过（-1，0）、（0，-3）两点和（4，1）（-2，3）两点；设y₁=k₁x+b₁，y₂=k₂x+b₂，代入可求出k₁、b₁和yk₂、b₂的值，然后，解二元一次方程组即可；
解答：由图得，函数y₁、y₂的图象l₁、l₂，分别过（-1，0）、（0，-3）两点和（4，1）（-2，3）两点，
∴，，
∴解得，，，
∴二元一次方程组为，
解得，．
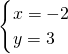故答案为：．
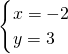点评：本题考查了一次函数与二元一次方程组的解法，从坐标系中能够得到两个一次函数经过的点的坐标，并求出函数的解析式，是解答本题的关键．