题目内容
 如图,AB∥DE,BC∥FG,∠1=56°25′,∠2=104°37′,求∠ABF的度数.
如图,AB∥DE,BC∥FG,∠1=56°25′,∠2=104°37′,求∠ABF的度数.
 解:延长AB,GF相交于点K,
解:延长AB,GF相交于点K,∵AB∥DE,∠1=56°25′,
∴∠BKF=∠1=56°25′,
∵∠2是△BFK的外角,
∴∠FBK=∠2-∠1=104°37′-56°25′=48°12′,
∴∠ABF=180°-∠FBK=180°-48°12′=131°48°.
分析:延长AB,GF相交于点K,根据AB∥DE可知∠BKF=∠1,再由三角形外角的性质可得出∠FBK的度数,根据平角的定义即可得出结论.
点评:本题考查的是平行线的性质,根据题意作出辅助线,构造出三角形是解答此题的关键.

练习册系列答案
相关题目
 如图,AB∥DE,BC∥EF,则①
如图,AB∥DE,BC∥EF,则①| OA |
| OD |
| OB |
| OE |
| OC |
| OF |
| OB |
| OE |
| A、① | B、② | C、①② | D、①②③ |
 7、如图,AB∥DE,∠E=65°,则∠B+∠C=( )
7、如图,AB∥DE,∠E=65°,则∠B+∠C=( )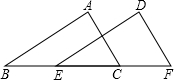 已知:如图,AB∥DE,且AB=DE.
已知:如图,AB∥DE,且AB=DE. 9、如图,AB∥DE,∠E=65°,则∠B+∠C=
9、如图,AB∥DE,∠E=65°,则∠B+∠C= 已知:如图,AB=DE,CD=FA,∠A=∠D,∠AFC=∠DCF,则BC=EF.你能说出它们相等的理由吗?
已知:如图,AB=DE,CD=FA,∠A=∠D,∠AFC=∠DCF,则BC=EF.你能说出它们相等的理由吗?