题目内容
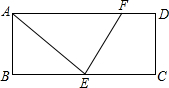长方形ABCD中，E是BC中点，作∠AEC的角平分线交AD于F点，若AB=3，AD=8，则FD的长度为
- A.2
- B.3
- C.4
- D.5
B
分析：求出∠AFE=∠AEF，推出AE=AF，求出BE，根据勾股定理求出AE，即可求出AF，即可求出答案．
解答：∵四边形ABCD是矩形，
∴AD=BC=8，AD∥BC，
∴∠AFE=∠FEC，
∵EF平分∠AEC，
∴∠AEF=∠FEC，
∴∠AFE=∠AEF，
∴AE=AF，
∵E为BC中点，BC=8，
∴BE=4，
在Rt△ABE中，AB=3，BE=4，由勾股定理得：AER=5，
∴AF=AE=5，
∴DF=AD-AF=8-5=3，
故选B．
点评：本题考查了矩形性质，平行线性质，等腰三角形的性质和判定的应用，注意：矩形的对边相等且平行．
分析：求出∠AFE=∠AEF，推出AE=AF，求出BE，根据勾股定理求出AE，即可求出AF，即可求出答案．
解答：∵四边形ABCD是矩形，
∴AD=BC=8，AD∥BC，
∴∠AFE=∠FEC，
∵EF平分∠AEC，
∴∠AEF=∠FEC，
∴∠AFE=∠AEF，
∴AE=AF，
∵E为BC中点，BC=8，
∴BE=4，
在Rt△ABE中，AB=3，BE=4，由勾股定理得：AER=5，
∴AF=AE=5，
∴DF=AD-AF=8-5=3，
故选B．
点评：本题考查了矩形性质，平行线性质，等腰三角形的性质和判定的应用，注意：矩形的对边相等且平行．
练习册系列答案
相关题目
如图，在长方形ABCD中AB=12cm，AD=8cm，点P，Q都从点A出发，分别沿AB和AD运动，且保持AP=AQ，在这个变化过程中，图中的阴影部分的面积也随之变化．当AP由2cm变到8cm时，图中阴影部分的面积是增加了，还是减少了？增加或减少了多少平方厘米？
8、如图，已知长方形ABCD中AB=8 BC=10，在边CD上取一点E，将△ADE折叠使点D恰好落在BC边上的点F，则DE的长为（ ）
；
长方形ABCD中，DP平分∠ADC交BC于P点，将一个直角三角板的直角顶点放在P点处，并使它的一条直角边过A点，另一条直角边交CD于E点．