如图.在平面直角坐标系中．直线y=﹣x+3与x轴交于点B.与y轴交于点C.抛物线y=ax2+bx+c经过B.C两点.与x轴负半轴交于点A.连结AC.A(1)求抛物线的解析式,是抛物线上在第一象限内的一点.求四边形OCPB面积S关于m的函数表达式及S的最大值,(3)若M为抛物线的顶点.点Q在直线BC上.点N在直线BM上.Q.M.N三点构成以MN为底边的等腰直角三角形.求点N的坐标．题目和参考答案——青夏教育精英家教网——

题目内容

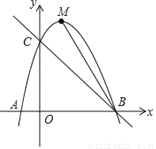
如图，在平面直角坐标系中．直线y=﹣x+3与x轴交于点B，与y轴交于点C，抛物线y=ax2+bx+c经过B，C两点，与x轴负半轴交于点A，连结AC，A(-1,0)

（1）求抛物线的解析式；

（2）点P（m，n）是抛物线上在第一象限内的一点，求四边形OCPB面积S关于m的函数表达式及S的最大值；

（3）若M为抛物线的顶点，点Q在直线BC上，点N在直线BM上，Q，M，N三点构成以MN为底边的等腰直角三角形，求点N的坐标．

（1）y==﹣x2+2x+3；（2）S=﹣（m﹣）2+，当m=时，S有最大值是；（3）点N的坐标为（2，2）或（﹣1，8）【解析】试题分析：（1）先根据直线BC的解析式求出点B和C的坐标，再利用待定系数法求抛物线的解析式；（2）作高线PE，利用面积和求四边形OCPB面积S，并配方成顶点式，求其最值；（3）先将抛物线配方成顶点式求M（1，4），利用待定系数法求直线MB的解析式...

练习册系列答案

全程考评期末一卷通系列答案

小学课堂练习合肥工业大学出版社系列答案

高中总复习导与练系列答案

随堂1加1导练系列答案

零距离学期系统总复习期末暑假衔接合肥工业大学出版社系列答案

期末冲刺100分创新金卷完全试卷系列答案

北大绿卡刷题系列答案

五州图书超越假期暑假内蒙古大学出版社系列答案

冲刺名校小考系列答案

黄冈中考考点突破系列答案

相关题目

完成下面的证明：

如图，AB和CD相交于点O，∠C＝∠COA，∠D＝∠BOD.

求证：∠A＝∠B.

见解析【解析】试题分析：先根据题意得出∠C=∠D，再由平行线的性质即可得出结论．试题解析：证明：∵∠C＝∠COA，∠D＝∠BOD(已知)，又∵∠COA＝∠BOD(__对顶角相等__)， ∴∠C＝__∠D__(等量代换)， ∴AC∥__BD__(__内错角相等，两直线平行__)， ∴∠A＝∠B(__两直线平行，内错角相等__)．

如图是由6个相同的小正方体搭成的几何体，那么这个几何体的俯视图是(　　)

C 【解析】【解析】从上面可看到第一横行左下角有一个正方形，第二横行有3个正方形，第三横行中间有一个正方形．故选C．

五个城市的国际标准时间（单位：时）在数轴上表示如图所示．对应于北京时间2009年1月1日上午10时这一时刻，下列说法错误的是（　　）

A. 伦敦时间为2009年1月1日凌晨2时

B. 纽约时间为2008年12月31日晚上20时

C. 圣多明各时间为2008年12月31日晚上22时

D. 首尔时间为2009年1月1日上午11时

B 【解析】根据北京时间求出每个地方的时间，求出两地的时差，判断可得： A、∵伦敦时间与北京差：8﹣0=8个小时，10﹣8=2， ∴当北京时间2009年1月1日10时，伦敦时间是2009年1月2日2时，故本选项不符合题意； B、∵纽约时间与北京差：8+5=13个小时，10﹣13=﹣3， ∴当北京时间2009年1月1日10时，纽约时间是2008年12月31日21时，故本...

某校的校门口立着一块告示牌“大门左右两侧50米以内不得设摊”，如果在数轴上以原点代表大门，用线段AB表示这一范围，那么A、B两点代表的数字是（　　）

A．-25，25 B．-50，50 C．0，50 D．-50，0

D 【解析】【解析】数轴上以原点代表大门，则A、B表示到原点距离是50米的点，即绝对值是50米的点，据此即可判断，故选D．

如图，在10×10的正方形网格中（每个小正方形的边长都为1个单位），△ABC的三个顶点都在格点上．建立如图所示的直角坐标系，

请在图中标出△ABC的外接圆的圆心P的位置，并填写：圆心P的坐标：P（ , ）

（2）将△ABC绕点A逆时针旋转90°得到△ADE，画出图

形，并求△ABC扫过的图形的面积．

（1）P（ 5 ， 3 ）（2）【解析】试题分析：（1）由外心是三角形各边垂直平分线的交点可知，我们在方格纸中画出AB和BC两边的垂直平分线就可找到外心，并得到其坐标；（2）如图，在旋转过程中，△ABC扫过的面积=S扇形ACE+S△ABC，因此我们只需要利用图中的信息由勾股定理计算出AC的长就可计算了. 试题解析：（1）如图，利用图中的格点分别画出线段AB和...

如图，在“3×3”网格中，有3个涂成黑色的小方格．若再从余下的6个小方格中随机选取1个涂成黑色，则完成的图案为轴对称图案的概率是______．

．【解析】试题分析：有6种等可能的结果，符合条件的只有2种，则完成的图案为轴对称图案的概率是. .

–3的绝对值是______________，倒数是________,相反数是_______.

3 - 3 【解析】–3的绝对值是3，倒数是 ,相反数是3.

.在△ABC中，，，直线经过点，且于，于.

(1)当直线绕点旋转到图1的位置时，的数量关系是_________________ ，并请给出证明过程.

(2)当直线绕点旋转到图2的位置时，的数量关系是_________________ （直接写出结果）。

（1）DE=AD+BE，理由见解析；（2）DE=AD﹣BE 【解析】试题分析：（1）由已知推出∠ADC=∠BEC=90°，因为∠ACD+∠BCE=90°，∠DAC+∠ACD=90°，推出∠DAC=∠BCE，根据AAS可证明△ADC≌△CEB（AAS），依据全等三角形的性质可得到AD=CE，CD=BE，然后由ED=DC+CE可得到问题的答案；（2）与（1）证法类似可证出∠ACD=∠EB...