题目内容
过点(-2,1)的反比例函数关系式是( )
A、y=
| ||
B、y=-
| ||
| C、y=-2x | ||
| D、y=2x |
考点:待定系数法求反比例函数解析式
专题:计算题
分析:利用待定系数法求解析式.
解答:解:设反比例函数解析式y=
,
把(-2,1)代入得k=-2×1=-2,
所以反比例函数解析式为y=-
.
故选B.
| k |
| x |
把(-2,1)代入得k=-2×1=-2,
所以反比例函数解析式为y=-
| 2 |
| x |
故选B.
点评:本题考查了待定系数法求反比例函数的解析式:设出含有待定系数的反比例函数解析式y=
(k为常数,k≠0);把已知条件(自变量与函数的对应值)代入解析式,得到待定系数的方程;解方程,求出待定系数;写出解析式.
| k |
| x |

练习册系列答案
相关题目
下列计算①32=3×2;②(-3)2=9;③-24=(-2)4;④(-3)2=
,正确的有( )
| 9 |
| 4 |
| A、1个 | B、2个 | C、3个 | D、4个 |
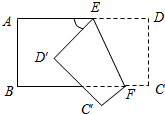 如图,把一张长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,若∠AED′=50°,则∠D′EF等于( )
如图,把一张长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,若∠AED′=50°,则∠D′EF等于( )| A、50° | B、55° |
| C、60° | D、65° |
某商品原价为28元,连续两次降价后售价为22.68元,若两次降价的百分率相同,那么这两次降价的百分率均为( )
| A、8.1% | B、9% |
| C、90% | D、10% |
六棱柱由几个面围成( )
| A、6个 | B、7个 | C、8个 | D、9个 |
 如图所示是一次函数y=mx+n的图象,当x≥0时,则( )
如图所示是一次函数y=mx+n的图象,当x≥0时,则( )| A、y≥0 | B、y≥2 |
| C、y≥1 | D、y≤2 |
 矩形OBCD按如图所示放置在平面直角坐标系中(坐标原点为O),连结AC
矩形OBCD按如图所示放置在平面直角坐标系中(坐标原点为O),连结AC