Question

若函数f(x)=-

1

2

x2+

13

3

当a≤x≤b时的最小值为2a，最大值为2b，求a、b的值．

Answer 1

分析：根据二次函数的增减性以及当a＜b≤0时，当a≤0＜b时，若0＜a＜b时分别得出a，b的值即可．

解答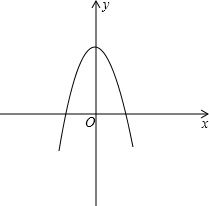：解：函数f(x)=-

1

2

x2+

13

3

的顶点是（0，

13

3

），对称轴是y轴，最大值为

13

3

，如右图，
（1）当a＜b≤0时，x=a时有最小值2a，x=b时有最大值2b，于是
-

1

2

a²+

13

3

=2a，
-

1

2

b²+

13

3

=2b，
可知a、b是方程-

1

2

x²+

13

3

=2x的两个根，
即3x²+12x-26=0，由于△＞0，x₁x₂=-

26

3

，
此方程有一正一负两个根，这与a＜b≤0矛盾，故此情况舍去；

（2）当a≤0＜b时，x=0时有最大值

13

3

=2b，
解得b=

13

6

，
x=b时有最小值2a，
即-

1

2

×（

13

6

）²+

13

3

=

143

72

＞0，而2a≤0，矛盾，
所以只能是x=a时取最小值，
（-

1

2

）a²+

13

3

=2a，
3a²+12a-26=0 a=

-6- 114

3

＜0，符合条件，

（3）若0＜a＜b，显然有 （-

1

2

）a²+

13

3

=2b①，
-

1

2

b²+

13

3

=2a②，
①-②得：（-

1

2

）（a-b）（a+b）=2（b-a），
则 a+b=4，
b=4-a，代入①得：（-

1

2

）a²+

13

3

=2（4-a），
3a²-12a+22=0，
∵△＜0，
∴此方程无实数根，故此情况舍去．
故有一组解符合要求：a=

-6- 114

3

，b=

13

6

．

点评：此题主要考查了二次函数的最值求法，根据自变量的取值范围分别将a，b代入求出是解题关键．