题目内容
3. 如图,△ABC为等边三角形,点D为BC边上的中点,DF⊥AB于点F,点E在BA的延长线上,且ED=EC,若AE=2,则AF的长为( )
如图,△ABC为等边三角形,点D为BC边上的中点,DF⊥AB于点F,点E在BA的延长线上,且ED=EC,若AE=2,则AF的长为( )| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{3}$+1 | D. | 3 |
分析 过点E作EH∥AC交BC的延长线于H,证明△ABH是等边三角形,求出CH,得到BD的长,根据直角三角形的性质求出BF,计算即可.
解答 解: 过点E作EH∥AC交BC的延长线于H,
过点E作EH∥AC交BC的延长线于H,
∴∠H=∠ACB=60°,又∠B=60°,
∴△EBH是等边三角形,
∴EB=EH=BH,
∴CH=AE=2,
∵ED=EC,
∴∠EDC=∠ECD,又∠B=∠H,
∴∠BED=∠HEC,
在△BED和△HEC中,
$\left\{\begin{array}{l}{EB=EH}\\{∠BED=∠HEC}\\{ED=EC}\end{array}\right.$,
∴△BED≌△HEC,
∴BD=CH=2,
∴BA=BC=4,BF=$\frac{1}{2}$BD=1,
∴AF=3.
故选:D.
点评 本题考查的是等边三角形的性质、直角三角形的性质以及等腰三角形的性质,掌握直角三角形中,30°角所对的直角边等于斜边的一半、等边三角形的三个角都是60°是解题的关键.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
15.下列命题正确的是( )
| A. | 若两条弧的长相等,则这两条弧是等弧 | |
| B. | 两条弧的长相等,它们所对的圆心角也相等 | |
| C. | 两个相等的圆心角所对的两条弧的长相等 | |
| D. | 如果两个圆的周长相等,那么它们的半径也相等 |
 如图,AB=AD,AC=AE,∠1=∠2,则下列正确结论有(1)(2)(4)(只填序号).
如图,AB=AD,AC=AE,∠1=∠2,则下列正确结论有(1)(2)(4)(只填序号).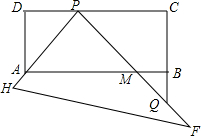 如图,有一块塑料矩形模板ABCD,AB=5cm,AD=2cm,将足够大的直角三角形PHF的直角顶点P落在CD边上(不与C、D重合),在CD上适当移动三角板顶点P,使直角边PH始终通过点A,另一直角边PF与CB的延长线交于点Q,与AB交于点M.若BM=1cm,则DP=2 cm.
如图,有一块塑料矩形模板ABCD,AB=5cm,AD=2cm,将足够大的直角三角形PHF的直角顶点P落在CD边上(不与C、D重合),在CD上适当移动三角板顶点P,使直角边PH始终通过点A,另一直角边PF与CB的延长线交于点Q,与AB交于点M.若BM=1cm,则DP=2 cm. 如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AD=6,则CP的长为3.
如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AD=6,则CP的长为3.




