Question

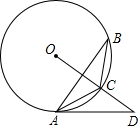已知：如图示，△ABC是⊙O的内接三角形，点D在OC的延长线上，∠B=∠CAD=30°，求证：AD是⊙O的切线．

Answer 1

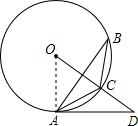证明：连OA，如图；
∵∠B=30°，
∴∠AOC=60°．
又∵∠CAD=30°，
∴∠OAD=90°．
∴AD是⊙O的切线．
分析：要证AD是⊙O的切线，要证明OA⊥AD，由∠B可求出∠AOC，从而得到∠OAD=90°．
点评：掌握切线的判定定理，知道证明圆的切线问题转化为证明线段垂直的问题，熟练运用圆周角定理．