题目内容
19. 在矩形ABCD中,AB=3米,BC=4米,动点P以2米/秒的速度从点A出发,沿AC向点C移动,同时动点Q以1米/秒的速度从点C出发,沿CB向点B移动,设P、Q两点同时移动的时间为t秒(0<t<2.5).
在矩形ABCD中,AB=3米,BC=4米,动点P以2米/秒的速度从点A出发,沿AC向点C移动,同时动点Q以1米/秒的速度从点C出发,沿CB向点B移动,设P、Q两点同时移动的时间为t秒(0<t<2.5).(1)当t为何值时,PQ∥AB;
(2)设四边形ABQP的面积为y,当t为何值时,y的值最小?并求出这个最小值.
分析 (1)首先由勾股定理求得AC=5,然后根据AB∥PQ可得到$\frac{PC}{AC}=\frac{QC}{BC}$,从而得到关于t的方程,从而可解得t的值;
(2)过点P作PE⊥BC,由PE∥AB可得到$\frac{PC}{AC}=\frac{PE}{AB}$,从而可求得PE=3-$\frac{6}{5}t$,然后根据y=△ABC的面积-△PQC的面积列出t与y的函数关系式,最后利用配方法求得最小值即可.
解答 解:(1)如图1所示: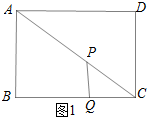
在Rt△ABC中,AC=$\sqrt{A{B}^{2}+B{C}^{2}}=\sqrt{{3}^{2}+{4}^{2}}=5$.
设运动时间为t,则PC=AC-AP=5-2t,QC=t,
∵AB∥PQ,
∴△CPQ∽△CAB.
∴$\frac{PC}{AC}=\frac{QC}{BC}$,$\frac{5-2t}{5}=\frac{t}{4}$.
解得;t=$\frac{20}{13}$;
(2)如图2所示:过点P作PE⊥BC.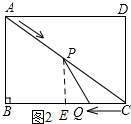
设运动时间为t,则PC=AC-AP=5-2t,QC=t,
∵PE∥AB,
∴△CPE∽△CAB.
∴$\frac{PC}{AC}=\frac{PE}{AB}$,即$\frac{5-2t}{5}=\frac{PE}{3}$.
∴PE=3-$\frac{6}{5}t$.
∴△PQC的面积=$\frac{1}{2}QC•PE=\frac{1}{2}×t(3-\frac{6}{5}t)$=-$\frac{3}{5}{t}^{2}+\frac{3}{2}t$.
∴y=△ABC的面积-△PQC的面积=$\frac{1}{2}×4×3$$-(-\frac{3}{5}{t}^{2}+\frac{3}{2}t)$=$\frac{3}{5}{t}^{2}-\frac{3}{2}t+6$,
配方得:y=$\frac{3}{5}(t-\frac{5}{4})^{2}+\frac{81}{16}$.
∴当t=$\frac{5}{4}$时,y有最小值,最小值为y=$\frac{81}{16}$.
点评 本题主要考查的是二次函数和相似三角形的性质和判定的综合应用,利用相似三角形的性质求得PE的长,从而得到y与t的函数关系式是解题的关键.

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案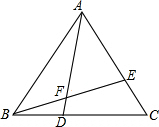 如图,已知在等边△ABC中,点D、E分别在BC,AC上,BD=CE,AD与BE交于点F
如图,已知在等边△ABC中,点D、E分别在BC,AC上,BD=CE,AD与BE交于点F
 如图,$\widehat{AB}$的度数为90°,点C、D将$\widehat{AB}$三等分,弦AB与半径OC、OD交于点E、F,求证:AE=CD=FB.
如图,$\widehat{AB}$的度数为90°,点C、D将$\widehat{AB}$三等分,弦AB与半径OC、OD交于点E、F,求证:AE=CD=FB.