题目内容
9.阅读理解:在平面直角坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“非常距离”,给出如下定义:若|x1-x2|≥|y1-y2|,则点P1与点P2的“非常距离”为|x1-x2|;
若|x1-x2|<|y1-y2|,则点P1与点P2的“非常距离”为|y1-y2|.
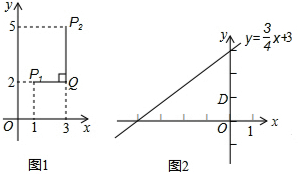
例如:点P1(1,2),点P2(3,5),因为|1-3|<|2-5|,所以点P1与点P2的“非常距离”为|2-5|=3,也就是图1中线段P1Q与线段P2Q长度的较大值(点Q为垂直于y轴的直线P1Q与垂直于x轴的直线P2Q的交点).
(1)已知点A(-$\frac{1}{2}$,0),B为y轴上的一个动点.
①若点B(0,3),则点A与点B的“非常距离”为3;
②若点A与点B的“非常距离”为2,则点B的坐标为(0,2)或(0,-2);
③直接写出点A与点B的“非常距离”的最小值$\frac{1}{2}$;
(2)已知点D(0,1),点C是直线y=$\frac{3}{4}$x+3上的一个动点,如图2,求点C与点D“非常距离”的最小值及相应的点C的坐标.
分析 (1)①根据若|x1-x2|<|y1-y2|,则点P1与点P2的“非常距离”为|y1-y2|解答即可;
②根据点B位于y轴上,可以设点B的坐标为(0,y).由“非常距离”的定义可以确定|0-y|=2,据此可以求得y的值;
③设点B的坐标为(0,y).因为|-$\frac{1}{2}$-0|≥|0-y|,所以点A与点B的“非常距离”最小值为|-$\frac{1}{2}$-0|=$\frac{1}{2}$;
(2)设点C的坐标为(x0,$\frac{3}{4}$x0+3).根据材料“若|x1-x2|≥|y1-y2|,则点P1与点P2的“非常距离”为|x1-x2|”知,C、D两点的“非常距离”的最小值为-x0=$\frac{3}{4}$x0+2,据此可以求得点C的坐标.
解答 解:(1)∵|-$\frac{1}{2}$-0|=$\frac{1}{2}$,|0-3|=3,
∴$\frac{1}{2}$<3,
∴点A与点B的“非常距离”为3.
故答案为:3;
②∵B为y轴上的一个动点,
∴设点B的坐标为(0,y).
∵|-$\frac{1}{2}$-0|=$\frac{1}{2}$≠2,
∴|0-y|=2,
解得,y=2或y=-2;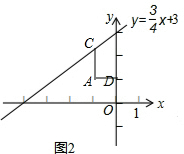
∴点B的坐标是(0,2)或(0,-2),
故答案为:(0,2)或(0,-2);
③点A与点B的“非常距离”的最小值为$\frac{1}{2}$.
故答案为:$\frac{1}{2}$;
(2)如图2,取点C与点D的“非常距离”的最小值时,
需要根据运算定义“若|x1-x2|≥|y1-y2|,则点P1与点P2的“非常距离”为|x1-x2|”解答,
此时|x1-x2|=|y1-y2|,即AC=AD,
∵C是直线y=$\frac{3}{4}$x+3上的一个动点,点D的坐标是(0,1),
∴设点C的坐标为(x0,$\frac{3}{4}$x0+3),
∴-x0=$\frac{3}{4}$x0+2,
此时,x0=-$\frac{8}{7}$,
∴点C与点D的“非常距离”的最小值为:|x0|=$\frac{8}{7}$,
此时C(-$\frac{8}{7}$,$\frac{15}{7}$).
点评 本题考查了一次函数综合题.对于信息给予题,一定要弄清楚题干中的已知条件.本题中的“非常距离”的定义是正确解题的关键.

| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
| A. | 直线$x=\frac{1}{4}$ | B. | 直线$x=-\frac{1}{4}$ | C. | y轴 | D. | x轴 |
 在平面直角坐标系中,已知两点A(2,0)和M(1,-1),过点M作直线l⊥x轴,直线l上有两动点E和F(点F在点M的上方),且ME=MF.
在平面直角坐标系中,已知两点A(2,0)和M(1,-1),过点M作直线l⊥x轴,直线l上有两动点E和F(点F在点M的上方),且ME=MF.