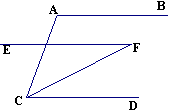
题目内容
 如图,已知EF∥CD,DE∥BC,下列结论中不一定正确的是
如图,已知EF∥CD,DE∥BC,下列结论中不一定正确的是
- A.

- B.
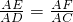
- C.

- D.

B
分析:“平行线分线段成比例”、等量代换对以下选项进行一一分析.
解答:A、∵EF∥CD,
∴ =
= ;
;
又∵DE∥BC,
∴ =
= ,
,
∴ =
= ;
;
故本选项正确;
B、当AE≠AF时, ≠
≠ ;故本选项错误;
;故本选项错误;
C、∵DE∥BC,
∴ =
= ;
;
又∵EF∥CD,
∴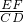 =
= ,
,
∴ ;
;
故本选项正确;
D、由A选项知: =
= ,则
,则 ;
;
故本选项正确;
故选B.
点评:本题考查了平行线分线段成比例.解题时,利用了平行线分线段成比例定理以及比例的性质进行变形.
分析:“平行线分线段成比例”、等量代换对以下选项进行一一分析.
解答:A、∵EF∥CD,
∴
 =
= ;
;又∵DE∥BC,
∴
 =
= ,
,∴
 =
= ;
;故本选项正确;
B、当AE≠AF时,
 ≠
≠ ;故本选项错误;
;故本选项错误;C、∵DE∥BC,
∴
 =
= ;
;又∵EF∥CD,
∴
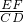 =
= ,
,∴
 ;
;故本选项正确;
D、由A选项知:
 =
= ,则
,则 ;
;故本选项正确;
故选B.
点评:本题考查了平行线分线段成比例.解题时,利用了平行线分线段成比例定理以及比例的性质进行变形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

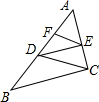 (2012•虹口区一模)如图,已知EF∥CD,DE∥BC,下列结论中不一定正确的是( )
(2012•虹口区一模)如图,已知EF∥CD,DE∥BC,下列结论中不一定正确的是( ) 如图,已知EF⊥CD于F,∠GEF=25°,∠1=65°,则AB与CD平行吗?请说明理由.
如图,已知EF⊥CD于F,∠GEF=25°,∠1=65°,则AB与CD平行吗?请说明理由. 如图,已知EF∥CD,∠1=∠2,请说明CD平分∠ACB的理由.
如图,已知EF∥CD,∠1=∠2,请说明CD平分∠ACB的理由.